About
RapidRMSD is a library for rapid computations of the root mean square deviations (RMSD) – an extension of our previous RigidRMSD library allowing for flexibility of molecules modeled with collective motions.
- The algorithm determines an exact set of RMSDs corresponding to flexible molecular motions in constant time with respect to the number of atoms in the molecule instead of quadratic time.
- It is particularly useful for flexible docking applications and for high-throughput analyses of modeling and simulation results.
Tests cases
Clustering
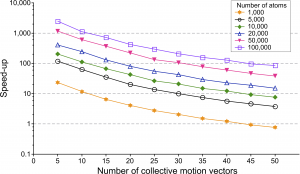
Speed-up given as time(standard method)/time(RapidRMS) as a function of the number of collective motion vectors in log-scale. Different curves correspond to a different number of atoms in the reference molecule.
We randomly generated flexible molecular docking poses for several molecules of a different size – on which we performed two clustering algorithms. Both algorithms use the same classification procedure but different ways to compute the RMSD: our approach is compared with the standard one.
Generation of pseudo-random structures of a fixed RMSD
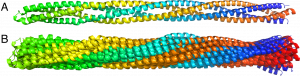
Constant-RMSD structural ensembles for a coiled-coil protein (PDB code 2ch7). The coiled coil is composed of two chains, each is colored from the N-terminus (blue) to the C-terminus (red). (A) The reference crystallographic structure is shown. (B) Ten pseudo-random structures are shown, each at RMSD of exactly 5 Å from the reference structure.
Another application of our method is the generation of pseudo-random structural ensembles along a few lowest normal modes. These structural ensembles can be useful to mimic molecular fluctuations at a constant temperature, or be used in machine-learning applications to mimic non-native docking poses
Methods
Molecular flexibility is described with linear collective motions. Collective motions are a linear transformation of the original structure, more precisely a weighted sum of orthogonal vectors, computed with, e.g., PCA or NMA methods.
Using the rigid-body motion formalism extended with collective motions, we express the RMSD between two molecules according to the spatial transformation operators : rotation, translation and the amplitudes of the collective motion vectors set of vectors.
This allows for a reduced computational time:
The initialisation step computational cost is at worst linear with the number of atoms and quadratic with the number of collective motion vectors. When one of the molecule is the rigid reference, it is linear with the number of atoms and linear with the number of collective motion vectors, whereas when the motion is purely flexible, this step costs nothing.
Then, each computation of RMSD takes at worst quadratic time with the number of collective motion vectors. When one of the molecule is the rigid reference or when the motions are purely flexible, it is linear with the number of collective motion vectors.
Since the number of collective motions is usually much lower than the number of atoms, RapidRMSD is particularly useful to compute multiple RMSDs.
Authors
Emilie Neveu, Petr Popov, Alexandre Hoffmann, and Sergei Grudinin,
NANO-D, INRIA Grenoble — Rhone-Alpes, 38334 Saint Ismier Cedex, Montbonnot, France.Laboratoire Jean Kuntzmann, B.P. 53, 38041 Grenoble Cedex 9, France.e-mail: Sergei.Grudinin @ inria.frDownload
License
This software is governed by the CeCILL-B license (fully BSD-compatible) under French law and abiding by the rules of distribution of free software.You can use, modify and/ or redistribute the software under the terms of the CeCILL-B license as circulated by CEA, CNRS and INRIA at this URL.
References
Emilie Neveu, Petr Popov, Alexandre Hoffmann, and Sergei Grudinin, “RapidRMSD : Rapid determination of RMSDs corresponding to motions of flexible molecules“. Submitted.
Alexandre Hoffmann, Sergei Grudinin. NOLB: Nonlinear Rigid Block Normal Mode Analysis Method . J. Chem. Theory Comp., 2017, 13 (5), pp.2123-2134. <10.1021/acs.jctc.7b00197>

Petr Popov and Sergei Grudinin, “Rapid determination of RMSDs corresponding to macromolecular rigid body motions”. J. Comput. Chem.2014, DOI: 10.1002/jcc.23569. Full text pdf.