| Method | Validation | Downloads | Tests | References |
About
Convex-PL is a knowledge-based scoring function for protein-ligand interactions.
Convex-PLR augments Convex-PL with conformational flexibility for better performance in affinity prediction and virtual screening tasks. It is trained on a more novel dataset that includes cofactors.
Method
Convex-PL
We suppose the interaction potential to be decomposed into a polynomial basis with expansion coefficients that can be found from a knowledge base with a convex optimization procedure. To do this, we assume that for a set of interaction sites located on the protein and ligand atoms, there is a linear functional dependent from the pairwise distances between the sites that indicates whether a configuration of a receptor-ligand complex is a native or a non-native one. The linear functional itself takes a simple form of a scalar product between a features “structure” vector and a scoring vector.
For a set of training protein-ligand complexes taken from the PDBBindCN 2015 database, we generate decoys with rigid-body deformations of ligand in the binding pocket preserving the ligand RMSD value. The training procedure includes the following stages (Fig. 1):
- Extraction of geometrical features, or the site-site distance distributions. For the typization of atomic sites we use our Knodle tool.
- These continuous features are projected into a set of discrete features.
- A Support Vector Machine quadratic optimization problem is solved to find the interaction potentials in form of a scoring vector.
To score an unknown configuration, a vector of its geometrical features is multiplied by the scoring vector, resulting in a relative binding energy prediction.
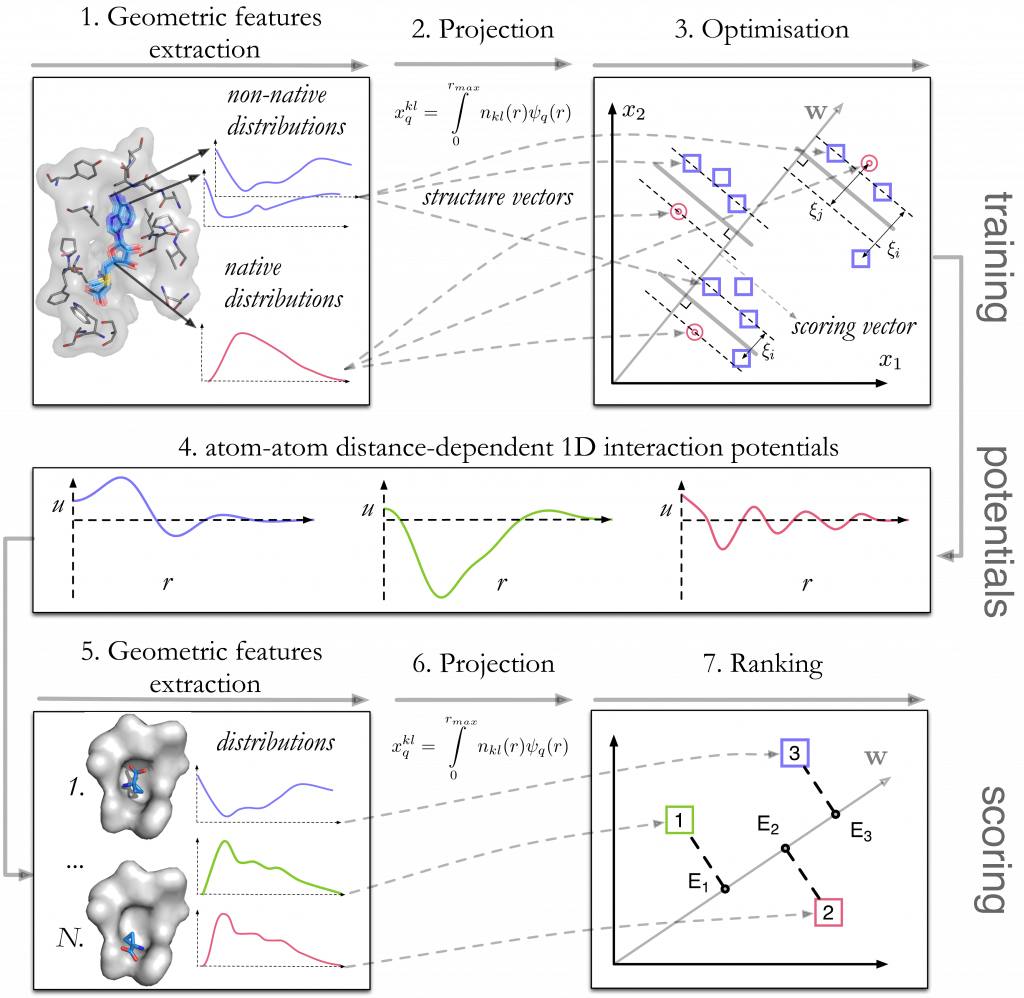
Figure 1. Schematic representation of the training stage (top) and the scoring stage (bottom) of the method.
Convex-PLR
To better account for the conformational entropy, we augmented Convex-PL with additional terms and trained their weights with a linear ridge regression model. An earlier version of Convex-PLR also includes desolvation terms based on solvent-accessible surface areas and interactions with meshes that represent displaced solvent.
VinaCPL
It is also possible to directly use Convex-PL for molecular docking. For this purpose, we created VinaCPL, where Convex-PL is integrated it as a scoring function into AutoDock
Vina. We suggest to use it in combination with the latest version of Convex-PL or with Convex-PLR for subsequent re-scoring. Specifically for re-scoring, we have modified the num_saved_min and num_modes parameters to get more output poses. It is also possible to provide a user-defined threshold for output poses clustering.
Validation
Convex-PL v0.2-v0.3
Method validation was done on the Comparative Assessment of Scoring Functions (CASF) 2013 benchmark. It included four tests that were already applied for 20 popular scoring functions assessment by the benchmark authors.
Compared to those 20 scoring functions, Convex-PL showed the best result in pose prediction, 5th result in the scoring test and 1st in ranking. Nevertheless, its results in the screening test representing the virtual screening tasks, which involve higher diversity of chemical compounds for each target receptor, were average.
Convex-PLR
Convex-PLR was validated on the CASF-2013 and 2016 benchmarks, on the tests generated from D3R user submissions, and on the DUD and LIT-PCBA virtual screening benchmarks. In the CASF benchmarks it showed top-ranked results in the pose prediction and scoring tests. Inclusion of additional descriptors improved its virtual screening abilities compared with Convex-PL. CASF-2013 and CASF-2016 test scores of Convex-PL v0.5 and Convex-PLR are available here.
On the DUD Benchmark Convex-PLR shows good results, outperforming AutoDock Vina and Vinardo. On LIT-PCBA Convex-PLR outperforms AutoDock Vina.
Download
Convex-PL v0.5 and Convex-PLR for Linux
Convex-PL v0.4 and Convex-PLR for Linux
Test cases
Convex-PL v0.2-v0.3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
user@host:~/convex-pl/convex-pl-test$ ../Convex-PL --receptor ./10gs/10gs_protein.pdb --ligand ./10gs/10gs_ligand.pdb #************************************************************ #*----------------------------------------------------------* #*------------------------Convex-PL-------------------------* #*-------------------------Authors:-------------------------* #*--Sergei Grudinin, Maria Kadukova, Georgy Cheremovskiy.---* #*-----Copyright (c): Nano-D team, Inria/CNRS Grenoble,-----* #*---------------France, Russia, 2011 - 2016.---------------* #*-------------e-mail: sergei.grudinin@inria.fr-------------* #*----------------------------------------------------------* #************************************************************ Number of decoys: 1 score = 35.4674971841729203 |
Convex-PL v0.5 and Convex-PLR
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
user@host: ./Convex-PL --receptor 4dli_protein.pdb --ligand 4dli_ligand.mol2 --mol2 --regscore #************************************************************ #*----------------------------------------------------------* #*------------------------Convex-PL-------------------------* #*-------------------------Authors:-------------------------* #*--Maria Kadukova, Georgy Cheremovskiy, Sergei Grudinin.---* #*-----Copyright (c): Nano-D team, Inria/CNRS Grenoble,-----* #*---------------France, Russia, 2011 - 2020.---------------* #*-------------e-mail: sergei.grudinin@inria.fr-------------* #*----------------------------------------------------------* #************************************************************ Number of decoys: 1 model 0, score = 6.34697516 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
user@host: ./Convex-PL --regscore --mol2 --receptor 2cpp_protein.pdb --ligand 2cpp_ligand.mol2 --cofactorList HEM:B:417 #************************************************************ #*----------------------------------------------------------* #*------------------------Convex-PL-------------------------* #*-------------------------Authors:-------------------------* #*--Maria Kadukova, Georgy Cheremovskiy, Sergei Grudinin.---* #*-----Copyright (c): Nano-D team, Inria/CNRS Grenoble,-----* #*---------------France, Russia, 2011 - 2020.---------------* #*-------------e-mail: sergei.grudinin@inria.fr-------------* #*----------------------------------------------------------* #************************************************************ Number of decoys: 1 model 0, score = 5.65690366 |
VinaCPL
References
- Convex-PL-R – Revisiting affinity predictions and virtual screening using physics-informed machine learning. Maria Kadukova, Vladimir Chupin, Sergei Grudinin. biorxiv pre-print, 2021 〈10.1101/2021.09.13.460049〉


- Convex-PL: a novel knowledge-based potential for protein-ligand interactions deduced from structural databases using convex optimization. Maria Kadukova, Sergei Grudinin. Journal of Computer-Aided Molecular Design, Springer Verlag, 2017, 〈10.1007/s10822-017-0068-8〉


- Docking of small molecules to farnesoid X receptors using AutoDock Vina with the Convex-PL potential: lessons learned from D3R Grand Challenge 2. Maria Kadukova, Sergei Grudinin. Journal of Computer-Aided Molecular Design, Springer Verlag, 2018, 32 (1), pp.151-162, 〈10.1007/s10822-017-0062-1〉


- Predicting Binding Poses and Affinities in the CSAR 2013―2014 Docking Exercises Using the Knowledge-Based Convex-PL Potential. Sergei Grudinin, Petr Popov, Emilie Neveu, Georgy Cheremovskiy. Journal of Chemical Information and Modeling, American Chemical Society, 2016, 56 (6), pp.1053-1062, 〈10.1021/acs.jcim.5b00339〉

- Predicting binding poses and affinities for protein-ligand complexes in the 2015 D3R Grand Challenge using a physical model with a statistical parameter estimation. Sergei Grudinin, Maria Kadukova, Andreas Eisenbarth, Simon Marillet, Frédéric Cazals. Journal of Computer-Aided Molecular Design, Springer Verlag, 2016, 30 (9), pp.791-804, 〈10.1007/s10822-016-9976-2〉






