High-Dimensional Regression with Gaussian Mixtures and Partially-Latent Response Variables
Statistics and Computing, Springer, 2015, vol. 25, number 5, pages 893-911
Antoine Deleforge, Florence Forbes and Radu Horaud
Abstract | arXiv | HAL| Springer | Supplementary materials | Slides | Citation and Bibtex
Associated software packages: Matlab toolbox | R code | Python/Keras package
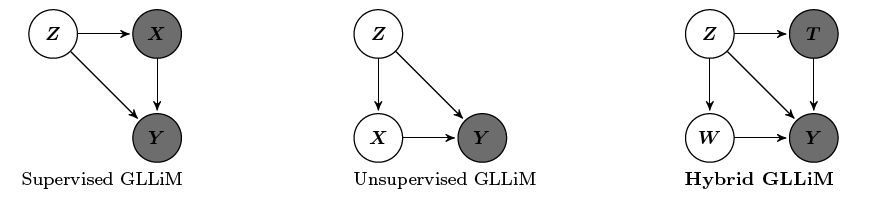
Abstract: The problem of approximating high-dimensional data with a low-dimensional representation is addressed. The article makes the following contributions. An inverse regression framework is proposed, which exchanges the roles of input and response, such that the low-dimensional variable becomes the regressor, and which is tractable. A mixture of locally-linear probabilistic mapping model is introduced, that starts with estimating the parameters of the inverse regression, and follows with inferring closed-form solutions for the forward parameters of the high-dimensional regression problem of interest. Moreover, a partially-latent paradigm is introduced, such that the vector-valued response variable is composed of both observed and latent entries, thus being able to deal with data contaminated by experimental artifacts that cannot be explained with noise models. The proposed probabilistic formulation could be viewed as a latent-variable augmentation of regression. Expectation-maximization (EM) procedures are introduced, based on a data augmentation strategy which facilitates the maximum-likelihood search over the model parameters. Two augmentation schemes are proposed and the associated EM inference procedures are described in detail; they may well be viewed as generalizations of a number of EM regression, dimension reduction, and factor analysis algorithms. The proposed framework is validated with both synthetic and real data. Experimental evidence is provided that the method outperforms several existing regression techniques.
A. Deleforge, F. Forbes and R. Horaud. High-Dimensional Regression with Gaussian Mixtures and Partially-Latent Response Variables. Statistics and Computing. Springer, 2015, 25 (5), pp. 893-911. 
E. Perthame, F. Forbes and A. Deleforge. Inverse Regression Approach to Robust Nonlinear High-to-Low Dimensional Mapping. Journal of Multivariate Analysis. Elsevier, 2018, 26(1), pp 1-14.
A. Deleforge, F. Forbes, S. Ba and R. Horaud. Hyper-Spectral Image Analysis with Partially-Latent Regression and Spatial Markov Dependencies. IEEE Journal on Selected Topics in Signal Processing, 2015, 9 (6), pp.1037-1048.

