Return to Projects

ERC PLEASE: Compressive Learning & More

Dates : 2012 – 2016 Funded : European Research Council Identifier: ERC-StG-2011-277906

Project Summary              Project Publications             Project Members

Projection, Learning, and Sparsity for Efficient data processing.

Sparse models are at the core of many research domains where the large amount and high-dimensionality of digital data requires concise data descriptions for efficient information processing. Recent breakthroughs have demonstrated the ability of these models to provide concise descriptions of complex data collections, together with algorithms of provable performance and bounded complexity.

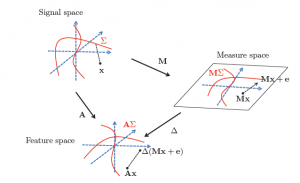
A flagship application of sparsity is the new paradigm of compressed sensing, which exploits sparsity for data acquisition using limited resources (e.g. fewer/less expensive sensors, limited energy consumption, etc.). Besides sparsity, a key pillar of compressed sensing is the use of random low-dimensional projections. While sparse models and random projections are at the heart of many success stories in signal processing and machine learning, their full long-term potential is yet to be achieved.

Some of the sub-topics investigated within PLEASE Project are listed below as clickable links.

Compressive Learning

Compressive sensing has been historically developed and successfully applied on sparse finite-dimensional signals, allowing to recover such signals from far fewer measurements than the ambient dimension. With the maturity of the theory has come the will to apply these paradigms to more general classes of signals, such as low-rank matrices, elements living in a general union of …

Graph Signal Processing

Nowadays, more and more data natively “live” on the vertices of a graph: brain activity supported by neurons in networks, traffic on transport and energy networks, data from users of social media, complex 3D surfaces describing real objects… Although graphs have been extensively studied in mathematics and computer science, a “signal processing” viewpoint on these …

Co-Sparsity and Sparse Analysis

Sparse analysis (cosparsity) is an alternative approach to sparse synthesis modelling that has emerged quite recently. For this model, we assume that the signal may be transferred into a low-dimensional space by using an appropriate analysis operator (such as the shift-invariant wavelet transform, for example). Being still a very hot research topic, cosparsity and its …

Sensor Calibration in Sparse Recovery

Compressed sensing theory shows that sparse signals can be sampled at a much lower rate than required by the Nyquist-Shannon theorem. Unfortunately, in some practical situations, it is sometimes not possible to perfectly know the exact characteristics of the sampling sensor. In many applications dealing with distributed sensors or radars, the location or intrinsic parameters …

Bayesian vs Regularization-based Approaches to Inverse Problems

There are two major routes to address linear inverse problems. Whereas regularization-based approaches build estimators as solutions of penalized regression optimization problems, Bayesian estimators rely on the posterior distribution of the unknown, given some assumed family of priors. While these may seem radically different approaches, recent results have shown that, in the context of linear …

Performance Limits of Ideal Decoders

Even though the standard sparse model of vectors has attracted much attention in linear inverse problems, other models with a low intrinsic dimension with respect to the ambient space have been considered in recent years. One can in particular cite low-rank matrices (with possible additional constraints), union of subspaces or more general manifold models. These …

Dictionary learning: theory and algorithms

Dictionary learning is a branch of signal processing and machine learning that aims at finding a frame (called dictionary) in which some training data admits a sparse representation. The sparser the representation, the better the dictionary. Efficient dictionaries. The resulting dictionary is in general a dense matrix, and its manipulation can be computationally costly both …