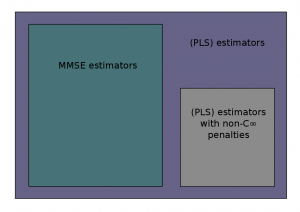
There are two major routes to address linear inverse problems. Whereas regularization-based approaches build estimators as solutions of penalized regression optimization problems, Bayesian estimators rely on the posterior distribution of the unknown, given some assumed family of priors. While these may seem radically different approaches, recent results have shown that, in the context of linear inverse problems with additive Gaussian noise, the Bayesian conditional mean estimator is always the solution of a penalized regression problem. With regards to sparse data and models, these results show that estimates provided by regularization-based approaches with sparsity-inducing penalty terms (i.e., non-smooth) cannot be optimal in a mean squared error sense. On a different note, a detailed analysis of the Bernoulli-Gaussian (hence sparse) signal models shows that conditional mean estimators cannot be associated with convex (penalized least squares) problems unless the sparsity level is low and the noise level is high.
For further details, please refer to the following publications: Should penalized least squares regression be interpreted as Maximum A Posteriori estimation? and Reconciling ”priors” and ”priors” without prejudice ?.