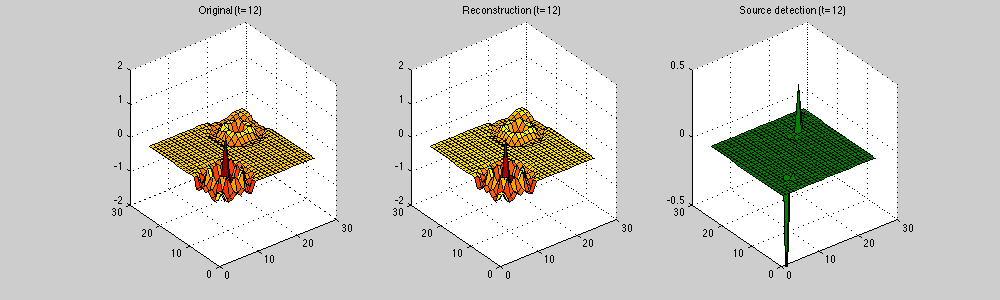
Sparse analysis (cosparsity) is an alternative approach to sparse synthesis modelling that has emerged quite recently. For this model, we assume that the signal may be transferred into a low-dimensional space by using an appropriate analysis operator (such as the shift-invariant wavelet transform, for example). Being still a very hot research topic, cosparsity and its applications are yet to be thoroughly understood. Cosparsity naturally arises in many physical problems modeled by linear partial differential equations. The model is encoded within the analysis operator which, when applied to the discretized physical quantity, yields sparse solution. The chosen applicative showcase for this application is the localization of sources in acoustic and EEG brain imaging contexts. The cosparse data model allows us to recover the entire sound field (or accordingly brain electrical field) by taking substantially small number of field measurements. The following picture shows the recovery of the full two-dimensional acoustic wave field, while recording data by only five microphones. The analysis model has potential to be used in wide spectrum of applications. To demonstrate this, we developed the audio declipping algorithm based on cosparsity which outperforms many state of the art approaches for the sound signal restoration.
For further information, please refer to the following publication: Hearing behind walls: localizing sources in the room next door with cosparsity.