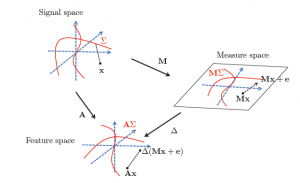
Even though the standard sparse model of vectors has attracted much attention in linear inverse problems, other models with a low intrinsic dimension with respect to the ambient space have been considered in recent years. One can in particular cite low-rank matrices (with possible additional constraints), union of subspaces or more general manifold models. These models have been proven, experimentally and/or theoretically, to grant nice reconstruction properties from certain linear measurements. This suggests the existence of well-behaved decoders with respect to a wide range of models in a linear inverse problem setting. In our work, we consider the classical property of instance optimality of a decoder. The existence of an instance optimal decoder with respect to any model can be expressed as a generalized null space property of the measurement operator. Building on this result, we provide links between a generalized Restricted Isometry Property and the existence of an instance optimal decoder. For further details, please refer to the following publication: Fundamental performance limits for ideal decoders in high-dimensional linear inverse problems.