Dictionary learning is a branch of signal processing and machine learning that aims at finding a frame (called dictionary) in which some training data admits a sparse representation. The sparser the representation, the better the dictionary.
Efficient dictionaries. The resulting dictionary is in general a dense matrix, and its manipulation can be computationally costly both at the learning stage and later in the usage of this dictionary, for tasks such as sparse coding. Dictionary learning is thus limited to relatively small-scale problems. Inspired by usual fast transforms, we proposed a general dictionary structure that allows cheaper manipulation, and an algorithm to learn such dictionaries –and their fast implementation– over training data. The approach was demonstrated experimentally with the factorization of the Hadamard matrix and with synthetic dictionary learning experiments. Further details can be found in the ICASSP 2015 paper Chasing butterflies: In search of efficient dictionaries, the EUSIPCO 2015 paper FA$\mu$ST: speeding up linear transforms for tractable inverse problems, and the paper Flexible Multi-layer Sparse Approximations of Matrices and Applications. Code to reproduce experiments in these papers is available at http://faust.gforge.inria.fr/
Sample complexity. Besides dictionary learning, many modern tools in machine learning and signal processing rely on the factorization of a matrix obtained by concatenating high-dimensional vectors from a training collection. While the idealized task would be to optimize the expected quality of the factors over the underlying distribution of training vectors, it is achieved in practice by minimizing an empirical average over the considered collection. In Sample Complexity of Dictionary Learning and other Matrix Factorizations, we provide sample complexity estimates to uniformly control how much the empirical average deviates from the expected cost function. The level of genericity of the approach encompasses several possible constraints on the factors (tensor product structure, shift-invariance, sparsity …), thus providing a unified perspective on the sample complexity of several widely used matrix factorization schemes.
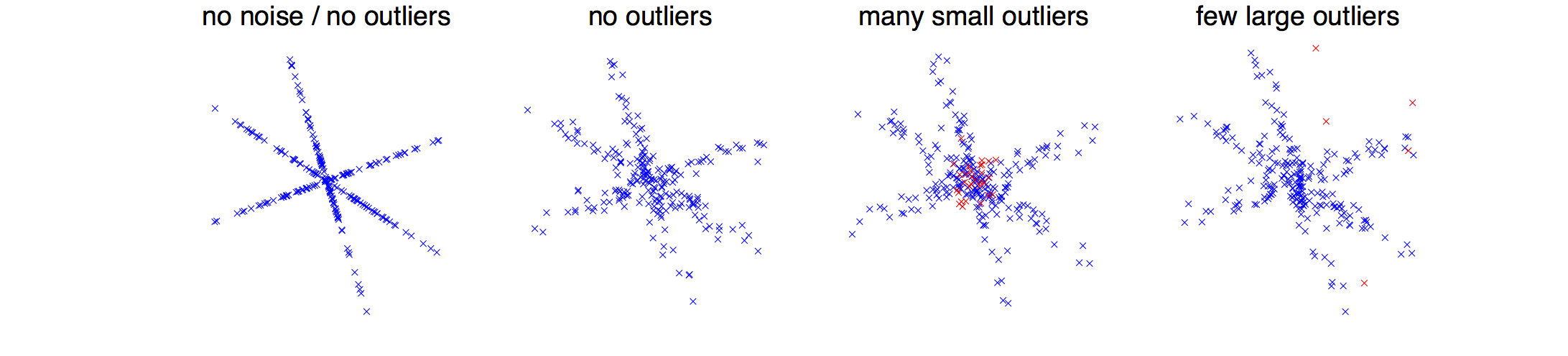
Provably good dictionary learning. Besides sample complexity issues, and important theoretical problem is to characterize the minima of the non-convex cost functions designed for dictionary learning. In Sparse and spurious: dictionary learning with noise and outliers we establish that, with high probability, sparse coding admits a local minimum around the reference dictionary generating the signals. Our study takes into account the case of over-complete dictionaries, noisy signals, and possible outliers, thus extending previous work limited to noiseless settings and/or under-complete dictionaries. The analysis is non-asymptotic and highlights the role of the key quantities of the problem, such as the coherence, the level of noise, the dimension of the signals, the number of atoms, the sparsity, and the number of observations.