- Title: Modélisation et Optimisation des réseaux sans fil: De l’usage des drones aux réseaux LoRaWAN (manuscript)
- When: March 27, 2024 — 14:00
- Where: Room 007, I3S laboratory
- Committee:
- André-Luc Beylot (referee), Toulouse INP ENSEEIHT, France
- Walid Dabbous, Inria, France
- Andrzej Duda, Grenoble INP Ensimag, France
- Isabelle Guérin-Lassous (referee), Université Lyon 1, France
- Samer Lahoud (referee), Dalhousie University, Canada
- Hervé Rivano, INSA Lyon, France
- Catherine Rosenberg, University of Waterloo, Canada
-
Résumé: Ce document retrace mes travaux sur la modélisation et l’optimisation des réseaux sans fil. J’applique des méthodes d’optimisation, principalement la programmation linéaire, pour calculer des solutions optimales et analyser leurs structures afin d’appliquer des techniques comme la génération de colonnes, ou évaluer des solutions approchées permettant de passer à l’échelle.
La première partie porte sur l’utilisation de drones afin de couvrir ou recharger des capteurs fixes ou mobiles. Les modèles optimisent le nombre de drones nécessaires ou calculent les trajectoires optimales. Les résultats mettent en évidence les compromis entre la distance parcourue en vol, l’énergie dépensée par les drones, et l’altitude impactant la qualité de couverture et de recharge.
La deuxième partie s’intéresse à la capacité des réseaux LoRaWAN en terme de nombre de nœuds tout en garantissant un taux de livraison des transmissions. J’optimise l’allocation des facteurs d’étalement et l’ordonnancement des transmissions dans des réseaux synchronisés tout en respectant les contraintes règlementaires d’utilisation de la bande de fréquence. Les résultats montrent l’intérêt du contrôle de puissance et de la répétition des envois de paquets.
Je conclus sur des perspectives autour de la dynamique des réseaux aériens, des nouvelles technologies pour les réseaux LPWAN, et des réseaux du futur virtualisés.
HDR defense of Emanuele Natale
- Title: Sur la somme de sous-ensembles aléatoires et quelques applications
- When: March 20, 2024 — 14:00
- Where: Room Euler Violet, Inria Sophia Antipolis Méditerranée
- Committee:
- Leszek GASIENIEC (referee), University of Liverpool, UK
- David PELEG (referee), Weizmann Institute of Science, Israel
- Christian SCHEIDELER (referee), University of Paderborn, Germany
- Pierluigi CRESCENZI Gran Sasso Science Institute, Italie
- Giovanni NEGLIA, Inria, France
- Laurent Viennot, Inria, Paris
-
Résumé: Cette présentation se concentre sur l’intersection du problème du sous-ensemble sléatoire (RSSP) et de ses applications novatrices au sein des réseaux de neurones artificiels (ANNs). Après un voyage rétrospectif qui couvre une décennie de recherche, l’exposé touche non seulement dans les contributions de l’auteur à la science informatique théorique, y compris les problèmes de consensus sous communication stochastique dans les systèmes multi-agents, mais s’aventure également dans les domaines de la modélisation d’évaluation intégrée et des explorations en neurosciences computationnelles. En synthétisant des intérêts de recherche allant de l’analyse stochastique des algorithmes distribués au développement d’algorithmes de pruning pour les ANNs, l’exposé vise à partager les contributions de l’auteur à la science informatique théorique et au-delà, en esquissant des orientations de recherche futures à l’intersection de l’informatique et d’autres sciences appliquées.
New team member : André Nusser
Welcome to our new team member: André Nusser.
André Nusser studied computer science at the University of Stuttgart, received his Ph.D. at the Max Planck Institute for Informatics in Saarbrücken (https://www.mpi-inf.mpg.de), where he was supervised by Karl Bringmann, then went to the University of Copenhagen (https://barc.ku.dk/) for a two year postdoc, and finally joined the the I3S laboratory and the COATI team as a CNRS researcher.
While his research interest is broadly in the field of algorithms, he has mainly focused on geometry, sprinkled with a little bit of graph algorithms, in the areas of classical algorithmics, fine-grained complexity theory, and algorithm engineering. He’s particularly interested in covering the whole spectrum from theory to the development of practically fast algorithms.
When he’s not doing research, you can find him climbing walls, playing music, highlining, juggling, or making poor attempts at acrobatics.
See his In’Tro seminar (March 18 2024).
PhD defense of Thomas Dissaux
- Title: “Graph decompositions: Treelength and pursuit-evasion games”
- When: September 25, 2023 — 14:00
- Where: Inria Sophia Antipolis, Euler violet
- Committee:
- Christophe Crespelle, Professor, Université Côte d’Azur, I3S, CNRS, France.
- Guillaume Ducoffe, Associate Professor, Faculty of Mathematics and Informatics, University of Bucharest, Romania.
- Arnaud Malapert, Maître de conférences, Université Côte d’Azur, I3S, CNRS, France.
- Cyril Gavoille (reviewer), Professor, LaBRI, Université de Bordeaux, France.
- Dimitrios M. Thilikos (reviewer), Directeur de recherche, LIRMM, Université de Montpellier, CNRS, Montpellier, France.
- Nicolas Nisse (supervisor), Chargé de recherche, Inria, Université Côte d’Azur, CNRS, I3S, Sophia-Antipolis, France.
-
Abstract: Graph decompositions are a powerful tool aimed to divide a graph into several parts, called bags, connected in a tree-like or a path-like fashion, depending on whether we consider a tree-decomposition or a path-decomposition. They can be used to solve some NP-hard problems in linear time, as long as the maximum size of the bags (i.e. the width) is bounded. This has motivated the study of treewidth (minimum width out of all tree-decompositions of a graph) over the past 30 years. Nevertheless, there are still a lot of open questions, such as the computational complexity of treewidth in planar graphs. To answer this question, it could be interesting to study the length of these decompositions. This measure corresponds to the maximum diameter among the bags of a decomposition, and it was shown that there is a relationship between treelength and treewidth in planar graphs.
In chapter 2, we study the treelength of several simple classes of planar graphs, such as series-parallel graphs. We give an infinite list of forbidden isometric subgraphs for series-parallel graphs of treelength 2. This list is then used to decide in polynomial time if a series-parallel graph has treelength at most 2 and, in case of a positive answer, to output a decomposition of length at most 2.
In chapter 3, we focus on the pathlength, and we give a characterization for trees and cycles. We also study the pathlength of outerplanar graphs for which we design an approximation algorithm with additive ratio 1.
Finally, in chapter 4, we study the Hunters and Rabbit game, an algorithmic variant of path-decomposition defined as a pursuit-evasion game. In this game, a group of hunters hunts an invisible rabbit which is forced to move to a neighboring position at every step. We are interested in the minimum number h(G) of hunters needed to catch the rabbit, independently of its moves along a graph G. This game has already been studied for some bipartite graphs (meshes, trees, hypercubes…). However, it remains open questions in a lot of graph classes, notably in trees. A very useful notion for the computation of strategies in pursuit-evasion games is the notion of monotonicity. We define a monotone variant of the Hunters and Rabbit game, for which we prove that the minimum number mh(G) of hunters differs by at most one from the pathwidth. This has important consequences, such as the fact that computing mh(G) is NP-hard. We also characterize mh(G) for several graph classes, such as split graphs, interval graphs, trees, and cographs. For these classes, we study the difference between mh and h and, in particular, we show that it is arbitrarily large in trees.
- Titre: “Décomposition de graphes: longueur arborescente et jeux de poursuite”
-
Résumé: Les décompositions de graphes sont un outil permettant de représenter un graphe en plusieurs parties, appelées sacs, et structurées comme un arbre ou un chemin suivant si ce sont des décompositions arborescentes ou linéaires. Ces décompositions permettent de résoudre certains problèmes NP-difficiles en temps linéaire, si la taille maximum des sacs (i.e. la « largeur/width ») est bornée. Cela a motivé les travaux de ces 30 dernières années sur la largeur arborescente d’un graphe G (la plus petite largeur des décompositions arborescente de G). Cependant, il reste encore beaucoup de questions ouvertes comme la complexité du calcul de la largeur arborescente des graphes planaires. Pour pouvoir répondre à cette question, il peut être intéressant d’étudier une autre mesure des décompositions, la longueur. Cette mesure correspond au diamètre maximum des sacs d’une décomposition, et il a été prouvé qu’il existe une relation entre la longueur arborescente et la largeur arborescente dans les graphes planaires.
Nous nous intéressons donc dans le chapitre 2 à la longueur arborescente de classes de graphes planaires simples, comme les graphes série-parallèles. Nous explicitons une liste infinie de sous-graphes isométriques interdits pour les graphes série-parallèles de longueur arborescente 2. Grâce à cette liste, il est alors possible en temps polynomial de tester si un graphe série-parallèle a une longueur arborescente au plus 2 et, dans le cas d’une réponse positive, de calculer une décomposition arborescente optimale.
Nous nous intéressons aussi au cas de la longueur linéaire dans le chapitre 3. Nous nous focalisons sur les classes des arbres et des cycles pour lesquelles nous caractérisons la longueur linéaire. Nous nous intéressons aussi à la longueur linéaire des graphes planaires extérieurs et concevons un algorithme d’approximation de rapport additif 1.
Finalement, dans le chapitre 4, nous nous intéressons à une variante algorithmique des décompositions linéaires des graphes, par le biais d’un jeu de poursuite-évasion, le jeu des Chasseurs et du Lapin. Dans ce jeu, un groupe de chasseurs traque un lapin invisible qui est forcé de bouger à chaque étape sur une position voisine. Nous nous intéressons au nombre minimum h(G) de chasseurs qui peuvent attraper le lapin quoi qu’il fasse sur un graphe G. Ce jeu a notamment été étudié dans le cas des graphes bipartis (grilles, arbres, hypercubes…) mais reste ouvert dans beaucoup de classes de graphes et notamment dans les arbres. Une notion très utile pour le calcul de stratégie dans les jeux de poursuite-évasion est la notion de monotonie. Nous définissons une variante monotone du jeu des chasseurs et du lapin, nous permettant entre autres, de prouver que, dans cette variante, le nombre minimum mh(G) de chasseurs diffère d’au plus un de la largeur linéaire du graphe G. Ce résultat a d’importantes conséquences, comme le fait que le calcul de mh(G) est NP-difficile. Nous caractérisons aussi mh(G) pour plusieurs classes de graphes, comme les graphes scindés, les graphes d’intervalles, les arbres et les cographes. Nous étudions la différence entre mh et h dans ces classes de graphes et, en particulier, nous montrons qu’il peut exister une différence arbitrairement grande entre mh et h dans les arbres.
PhD defense of Igor Dias da Silva
- Title: “Optimisation of UAVs deployment and coordination for exploration and monitoring applications”
- When: September 21, 2023 — 15:00
- Where: I3S, room 007, Les Algorithmes
- Committee:
- Emmanuel Chaput (reviewer), Professor, INP Toulouse, France.
- Enrico Natalizio (reviewer), Professor, LORIA, Université de Lorraine, Nancy, France.
- Hervé Rivano, Professor, INSA, Lyon, France.
- Yann Busnel, Professor, IMT Nord Europe, Lille, France.
- David Coudert, Directeur de Recherche, Centre Inria d’Université Côte d’Azur, France.
- Christelle Caillouet, Assistant Professor, Université Côte d’Azur, France.
-
Abstract: Unmanned Aerial Vehicles (UAVs) have gained tremendous attention lately. These autonomous flying devices have several advantages in terms of deployment cost and processing capabilities, making them a promising solution for a wide range of military and commercial applications. In this thesis, we have studied two applications: creating a flying network to connect mobile sensors to a base station and wirelessly charging fixed ground sensors.
In the first application, we want to communicate with mobile sensors in a disaster scenario without pre-existing communication infrastructure. Our goal in this application is to determine the optimal flight plans for the UAVs. The UAVs must maintain a connected path between the base station and the sensors to allow the sensors to send critical information when necessary. We optimise the UAVs’ total distance travelled and energy consumed.
The second application has a set of fixed ground sensors we need to recharge. Equipping the UAVs and sensors with power harvesting technology allows us to recharge these sensors wirelessly. We proposed a 2 step solution where first, a linear program finds where each drone needs to go and how long it should stay there to ensure the sensors get enough power. Then, greedy scheduling algorithms determine the order in which UAVs visit these spots, ensuring they do not get in each other’s way or reduce the charging efficiency. We minimise the total time to charge all sensors in both steps.
- Titre: “Optimisation du déploiement et de la coordination de drones pour les applications d’exploration et de surveillance”
-
Résumé: Les véhicules aériens sans pilote (UAV) ont suscité une attention considérable récemment. Ces appareils volants autonomes présentent plusieurs avantages en termes de coûts de déploiement et de capacités de traitement, ce qui en fait une solution prometteuse pour un large éventail d’applications militaires et commerciales. Dans cette thèse, nous avons étudié deux applications : la création d’un réseau aérien pour connecter des capteurs mobiles à une station de base et la recharge sans fil de capteurs fixes au sol.
Dans la première application, nous voulons communiquer avec des capteurs mobiles dans un scénario de catastrophe sans infrastructure de communication préexistante. Notre objectif dans cette application est de déterminer les meilleurs plans de vol pour les UAVs. Les UAVs doivent maintenir un chemin connecté entre la station de base et les capteurs pour permettre aux capteurs d’envoyer des informations critiques si nécessaire. Nous optimisons la distance totale parcourue par les UAVs et l’énergie consommée.
La deuxième application concerne un ensemble de capteurs au sol fixes que nous devons recharger. La technologie de récupération d’énergie, basée sur l’échange de signaux radio-fréquence, permettant de recharger les batteries des capteurs sans fil. Nous avons proposé une solution en 2 étapes où d’abord, un programme linéaire détermine où chaque drone doit aller et combien de temps il doit y rester pour s’assurer que les capteurs reçoivent suffisamment d’énergie. Ensuite, des algorithmes gloutons d’ordonnancement déterminent l’ordre dans lequel les UAVs visitent ces points, en veillant à ce qu’ils ne se gênent pas mutuellement ou ne réduisent pas l’efficacité de la charge. Nous minimisons le temps total nécessaire pour recharger tous les capteurs dans les deux étapes.
PhD defense of Arthur C. W. da Cunha
- Title: “Pruning random structures”
- When: September 13, 2023 — 14:00
- Where: Inria Sophia Antipolis, Euler violet
- Committee:
- Emanuele NATALE (Thesis director), Chargé de Recherche, CNRS, COATI, France.
- Vincent GRIPON (Reviewer), IMT-Atlantique, France.
- Marc LELARGE (Reviewer), Directeur de recherche, Inria, Paris, France.
- Konstantin AVRACHENKOV, Directeur de recherche, Inria, Sophia Antipolis, France.
- Pierluigi CRESCENZI, Professeur, Gran Sasso Science Institute, L’Aquila, Italy.
- Frédéric GIROIRE, Directeur de recherche, CNRS. COATI, Sophia Antipolis, France.
- Laurent VIENNOT (Invited), Directeur de recherche, Inria, Paris, France.
-
Abstract: The Strong Lottery Ticket Hypothesis (SLTH) states that neural networks contain, at random initialisation, sub-networks that perform well without any training. The random network needs, however, to be over-parameterized: to have more parameters than it would otherwise need.
The SLTH was first proved for fully-connected networks and assumed polynomial over-parameterization. Soon after, this was improved to only require a logarithmic overhead, which is essentially optimal. This strong result leveraged a theorem on the Subset Sum Problem (SSP). It considers a randomised version of the SSP in which one seeks to approximate a target value by summing subsets of a given random sample. The theorem asserts that ensuring the existence of a solution with high probability only requires a logarithmic sample size relative to the precision of the approximations. We present a simpler, more direct proof for this result.
Then, leveraging the theorem on the SSP, we extend the SLTH to Convolutional Neural Networks (CNNs): we show that random CNNs contain sparse sub-CNNs that do not require training to achieve good performance. We also obtained the result assuming a logarithmic over-parameterization.
Even though the overhead imposed by the SLTH could be offset by the sparsity of the sub-networks obtained, exploiting sparsity in practice is very difficult if it is not structured. Extending the results on the SLTH to produce structured sub-networks would require a multidimensional version of the theorem on SSP. We prove such a version and use it to show that the SLTH still holds for CNNs if we require the sub-networks to be structured.
Finally, we propose an application of the ideas in this thesis to the design of circuits: We harness the inherent randomness in the specs of integrated electronic components to obtain highly accurate programmable components from low-precision static ones.
- Titre: “Élagage de structures aléatoires”
-
Résumé: La Strong Lottery Ticket Hypothesis (SLTH) stipule que les réseaux de neurones contiennent, lors de l’initialisation aléatoire, des sous-réseaux qui fonctionnent bien sans aucun entraînement. Le réseau aléatoire doit cependant être sur-paramétré : avoir plus de paramètres qu’il n’en aurait besoin.
La SLTH a d’abord été prouvée pour les réseaux entièrement connectés et suppose une sur-paramétrisation polynomiale. Puis, cela a été amélioré pour ne nécessiter qu’un surplus logarithmique, ce qui est essentiellement optimal. Ce fort résultat a tiré parti d’un beau théorème sur le Subset Sum Problem (SSP). Il considère une version aléatoire du SSP dans laquelle on cherche à approximer une valeur cible en sommant des sous-ensembles d’un échantillon aléatoire donné. Le théorème affirme que garantir l’existence d’une solution avec une haute probabilité ne nécessite qu’une taille d’échantillon logarithmique par rapport à la précision des approximations. Nous présentons une preuve plus simple et plus directe pour ce résultat.
Ensuite, en tirant parti du théorème sur le SSP, nous étendons le SLTH aux Convolutional Neural Networks (CNNs) : nous montrons que les CNN aléatoires contiennent des sous-CNN clairsemés qui n’ont pas besoin d’entraînement pour obtenir de bonnes performances. Nous avons également obtenu le résultat en supposant une sur-paramétrisation logarithmique.
Bien que le surplus imposé par le SLTH puisse être compensé par la rareté des sous-réseaux obtenus, exploiter la rareté en pratique est très difficile si elle n’est pas structurée. Étendre les résultats sur le SLTH pour produire des sous-réseaux structurés nécessiterait une version multidimensionnelle du théorème sur le SSP. Nous prouvons la véracité d’une telle version et nous l’utilisons pour montrer que le SLTH est toujours valable pour les CNN si nous exigeons que les sous-réseaux soient structurés.
Enfin, nous proposons une application des idées de cette thèse à la conception de circuits : nous exploitons l’aléatoire inhérent aux spécifications des composants électroniques intégrés pour obtenir des composants programmables hautement précis à partir de composants statiques de faible précision.
In’Tro Emanuele Natale
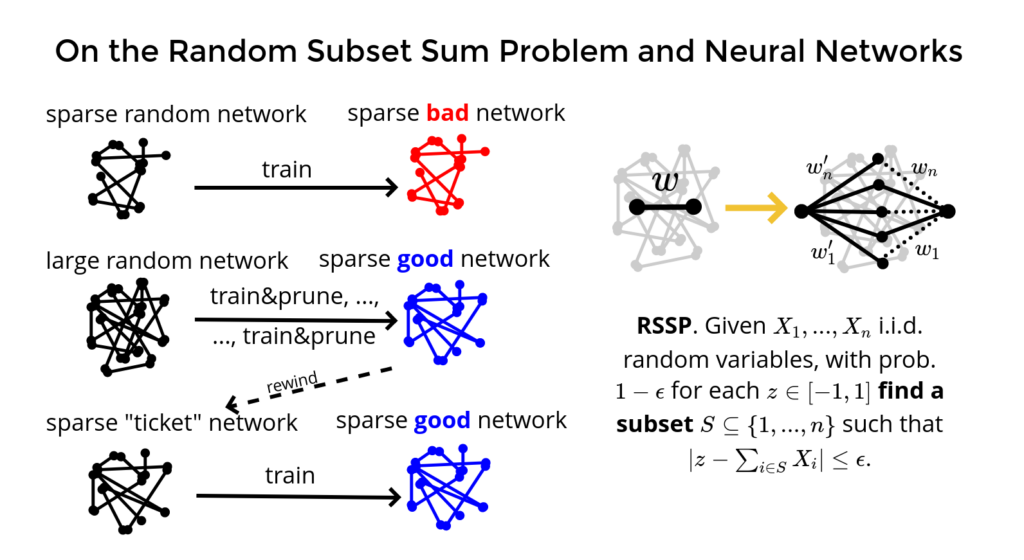
- Title: “On the Random Subset Sum Problem and Neural Networks”
- When: May 30, 2023 — 13:30
- Where: online seminar In’Tro
-
Abstract: The Random Subset Sum Problem (RSSP) is a fundamental problem in mathematical optimization, especially in understanding the statistical behavior of integer linear programs.
Recently, the theory related to this problem has also found applications in theoretical machine learning, providing key tools for proving the Strong Lottery Ticket Hypothesis (SLTH) for dense neural network architectures. In this talk, I will give a brief overview of this research direction and present my recent joint work that pushes the application of RSSP further by providing a proof of the SLTH for convolutional neural networks.
Un Palais de la Découverte des Sciences du numérique
Entretien avec Dorian Mazauric et Frédéric Havet sur le projet Terra Numerica pour le blog binaire du journal Le Monde.
PhD defense of Francesco d’Amore
- Title: “On the Collective Behaviors of Bio-Inspired Distributed Systems”
- When: October 17, 2022 — 14:00
- Where: Inria Sophia Antipolis, Euler violet
- Committee:
- Robert Elsässer (referee), Full Professor, University of Salzburg, Austria
- Pierre Fraigniaud (referee), Directeur de Recherche, CNRS, France
- Frederik Mallmann-Trenn (referee), Assistant Professor, King’s College London, United Kingdom
- Emanuele Natale (supervisor), Chargé de Recherche, CNRS, France
- Nicolas Nisse (supervisor), Chargé de Recherche, Inria, France
- Alain Jean-Marie, Directeur de Recherche, Inria, France
-
Abstract: In recent years there has been a surge of interest on behalf of the algorithmic community in applying its theoretical tools to the understanding of complex systems, in particular biological ones, such as insect colonies, flocks of birds, and networks of neurons. We contribute to the investigation of such systems in three different directions. First, we analyze computational dynamics for stochastic coordination tasks in multi-agent systems: in particular, we focus on the consensus problem in environments where communication is affected by some form of noise. In this setting, we analyze two known opinion dynamics, the \textsc{Undecided-State} and the \textsc{3-Majority} dynamics, and prove that they exhibit a phase-transition at different noise thresholds. Below the threshold, the two dynamics quickly reach an almost-consensus metastable phase; above, no form of consensus is possible. Second, we study Lévy walks, i.e.,\ special random walks known to model many movement patterns found in nature, characterized by a step-length density distribution proportional to a power-law. We analyze their parallel hitting time and show how to use them to design an almost optimal algorithm for the ANTS problem, a distributed search problem on $ \mathbb{Z}^2 $ which captures some aspects of animal foraging theory. Third, we consider the Assembly Calculus, a recently proposed distributed computational model of the brain which consists of stylized spiking neurons and synapses, and we test experimentally its capabilities, largely unexplored. In particular, we implement known heuristics for the Blocks World planning task; we empirically prove that reasonably large and complex programs in the Assembly Calculus run correctly and reliably.
- Titre: “Sur les Comportements Collectifs de Systèmes Distribués Bio-Inspirés”
-
Résumé:
Récemment, la communauté algorithmique a manifesté un intérêt croissant pour l’utilisation de ses outils théoriques à la compréhension des systèmes complexes, notamment biologiques, tels que les colonies d’insectes, les volées d’oiseaux et les réseaux de neurones. Nous contribuons à l’étude de ces systèmes dans trois directions différentes. Premièrement, nous analysons des dynamiques computationnelles pour les tâches de coordination stochastique dans les systèmes multi-agents. En particulier, nous nous focalisons sur le problème du consensus dans des environnements où la communication est bruyante : nous analysons deux dynamiques d’opinion, les dynamiques \textsc{Undecided-State} et \textsc{3-Majority}, et nous prouvons qu’elles présentent une transition de phase à des seuils de bruit différents. En dessous du seuil, ces dynamiques atteignent rapidement une phase métastable de quasi-consensus ; au-dessus, aucune forme de consensus n’est possible. Deuxièmement, nous étudions les Lévy walks, des marches aléatoires qui modélisent des schémas de mouvement trouvés dans la nature, dont la distribution de la longueur de pas suit une loi de puissance. Nous analysons leur temps d’arrêt (hitting time) parallèle et les utilisons pour concevoir un algorithme optimal pour l’ANTS problem, un problème de recherche distribuée sur $\mathbb{Z}^2$ qui capture certains aspects de la théorie du butinage. Troisièmement, nous considérons l’Assembly Calculus, un modèle distribué du cerveau récemment proposé, qui consiste en des neurones et des synapses stylisés, et nous testons expérimentalement ses capacités, largement inexplorées, en mettant en œuvre des heuristiques connues pour la tâche de planification du monde des blocs. Nous montrons empiriquement que des programmes grands et complexes dans ce modèle s’exécutent correctement et de manière fiable.
PhD defense of Hicham Lesfari
- Title: “Foundations of Networks towards AI”
- When: October 7, 2022 — 9:00
- Where: Inria Sophia Antipolis, Euler violet
- Committee:
- Andrea Clementi, Full Professor, University of Rome Tor Vergata
- Romuald Elie, Research Scientist, DeepMind, Google
- Frédéric Giroire (supervisor), Directeur de recherche, CNRS
- Marc Lelarge (referee), Directeur de recherche, Inria Paris
- Pietro Michiardi (referee), Full Professor, EURECOM
- Giovanni Neglia, Directeur de recherche, Inria Sophia Antipolis
-
Abstract: The field of Artificial Intelligence (AI) has brought a broad impact on today’s society, leading to a gripping interaction between several scientific disciplines. In this respect, there has been a strong twofold interest across the literature. On the one hand, a growing trend in telecommunication networks consists in revisiting classic optimization problems using machine learning techniques in order to exploit their potential benefits. We focus on some challenges brought by the detection of anomalies in networks, and the allocation of resources within software-defined networking (SDN) and network function virtualization (NFV). On the other hand, a substantial effort has been devoted towards the theoretical understanding of the collective behavior of networks. We focus on some challenges brought by the study of majority dynamics within multi-agent systems, and the compression of artificial neural networks with the aim at increasing their efficiency. In this study, we contextualize the above focal points in the framework of investigating some foundations of networks; viewed through the lens of telecommunications networks and neural networks. We first focus our attention on developing graph similarity measures for network anomaly detection. Next, we study deterministic and stochastic majority dynamics in multi-agent systems. Then, we discuss the random subset sum problem in the context of neural network compression. Finally, we walk through some other miscellaneous problems.
- Titre: “Fondements Réseaux et IA”
-
Résumé: Le domaine de l’Intelligence Artificielle (IA) a un large impact sur la société d’aujourd’hui, ayant conduit notamment à une interaction passionnante entre plusieurs disciplines scientifiques. À cet égard, un double intérêt émerge dans la littérature. D’une part, une tendance croissante dans les réseaux de télécommunication consiste à revisiter les problèmes d’optimisation classiques en utilisant des techniques d’apprentissage automatique afin d’exploiter leurs avantages potentiels. Nous nous focaliserons sur certains défis posés par la détection d’anomalies dans les réseaux ainsi que l’allocation des ressources dans le cadre des réseaux logiciels (SDN) et de la virtualisation des fonctions réseau (NFV). D’autre part, un effort substantiel a été consacré dans le but d’apporter une compréhension théorique du comportement collectif des réseaux. Nous nous focaliserons sur certains défis posés par l’étude de la dynamique majoritaire au sein des systèmes multi-agents ainsi qu’à la compression des réseaux de neurones artificiels dans le but d’augmenter leur efficacité. Dans cette étude, nous contextualisons les points focaux ci-dessus dans le cadre de l’étude de certains fondements de réseaux; vus sous l’angle des réseaux de télécommunications et des réseaux neuronaux. Nous nous concentrons d’abord sur le développement de mesures de similarité de graphes pour la détection d’anomalies dans les réseaux. Ensuite, nous étudions la dynamique majoritaire déterministe et stochastique dans les systèmes multi-agents. Ensuite, nous discutons du problème de la somme de sous-ensembles aléatoires dans le contexte de la compression des réseaux neuronaux. Enfin, nous passons en revue quelques problèmes généraux divers.