- Title: “Pruning random structures”
- When: September 13, 2023 — 14:00
- Where: Inria Sophia Antipolis, Euler violet
- Committee:
- Emanuele NATALE (Thesis director), Chargé de Recherche, CNRS, COATI, France.
- Vincent GRIPON (Reviewer), IMT-Atlantique, France.
- Marc LELARGE (Reviewer), Directeur de recherche, Inria, Paris, France.
- Konstantin AVRACHENKOV, Directeur de recherche, Inria, Sophia Antipolis, France.
- Pierluigi CRESCENZI, Professeur, Gran Sasso Science Institute, L’Aquila, Italy.
- Frédéric GIROIRE, Directeur de recherche, CNRS. COATI, Sophia Antipolis, France.
- Laurent VIENNOT (Invited), Directeur de recherche, Inria, Paris, France.
-
Abstract: The Strong Lottery Ticket Hypothesis (SLTH) states that neural networks contain, at random initialisation, sub-networks that perform well without any training. The random network needs, however, to be over-parameterized: to have more parameters than it would otherwise need.
The SLTH was first proved for fully-connected networks and assumed polynomial over-parameterization. Soon after, this was improved to only require a logarithmic overhead, which is essentially optimal. This strong result leveraged a theorem on the Subset Sum Problem (SSP). It considers a randomised version of the SSP in which one seeks to approximate a target value by summing subsets of a given random sample. The theorem asserts that ensuring the existence of a solution with high probability only requires a logarithmic sample size relative to the precision of the approximations. We present a simpler, more direct proof for this result.
Then, leveraging the theorem on the SSP, we extend the SLTH to Convolutional Neural Networks (CNNs): we show that random CNNs contain sparse sub-CNNs that do not require training to achieve good performance. We also obtained the result assuming a logarithmic over-parameterization.
Even though the overhead imposed by the SLTH could be offset by the sparsity of the sub-networks obtained, exploiting sparsity in practice is very difficult if it is not structured. Extending the results on the SLTH to produce structured sub-networks would require a multidimensional version of the theorem on SSP. We prove such a version and use it to show that the SLTH still holds for CNNs if we require the sub-networks to be structured.
Finally, we propose an application of the ideas in this thesis to the design of circuits: We harness the inherent randomness in the specs of integrated electronic components to obtain highly accurate programmable components from low-precision static ones.
- Titre: “Élagage de structures aléatoires”
-
Résumé: La Strong Lottery Ticket Hypothesis (SLTH) stipule que les réseaux de neurones contiennent, lors de l’initialisation aléatoire, des sous-réseaux qui fonctionnent bien sans aucun entraînement. Le réseau aléatoire doit cependant être sur-paramétré : avoir plus de paramètres qu’il n’en aurait besoin.
La SLTH a d’abord été prouvée pour les réseaux entièrement connectés et suppose une sur-paramétrisation polynomiale. Puis, cela a été amélioré pour ne nécessiter qu’un surplus logarithmique, ce qui est essentiellement optimal. Ce fort résultat a tiré parti d’un beau théorème sur le Subset Sum Problem (SSP). Il considère une version aléatoire du SSP dans laquelle on cherche à approximer une valeur cible en sommant des sous-ensembles d’un échantillon aléatoire donné. Le théorème affirme que garantir l’existence d’une solution avec une haute probabilité ne nécessite qu’une taille d’échantillon logarithmique par rapport à la précision des approximations. Nous présentons une preuve plus simple et plus directe pour ce résultat.
Ensuite, en tirant parti du théorème sur le SSP, nous étendons le SLTH aux Convolutional Neural Networks (CNNs) : nous montrons que les CNN aléatoires contiennent des sous-CNN clairsemés qui n’ont pas besoin d’entraînement pour obtenir de bonnes performances. Nous avons également obtenu le résultat en supposant une sur-paramétrisation logarithmique.
Bien que le surplus imposé par le SLTH puisse être compensé par la rareté des sous-réseaux obtenus, exploiter la rareté en pratique est très difficile si elle n’est pas structurée. Étendre les résultats sur le SLTH pour produire des sous-réseaux structurés nécessiterait une version multidimensionnelle du théorème sur le SSP. Nous prouvons la véracité d’une telle version et nous l’utilisons pour montrer que le SLTH est toujours valable pour les CNN si nous exigeons que les sous-réseaux soient structurés.
Enfin, nous proposons une application des idées de cette thèse à la conception de circuits : nous exploitons l’aléatoire inhérent aux spécifications des composants électroniques intégrés pour obtenir des composants programmables hautement précis à partir de composants statiques de faible précision.
Author: David COUDERT
In’Tro Emanuele Natale
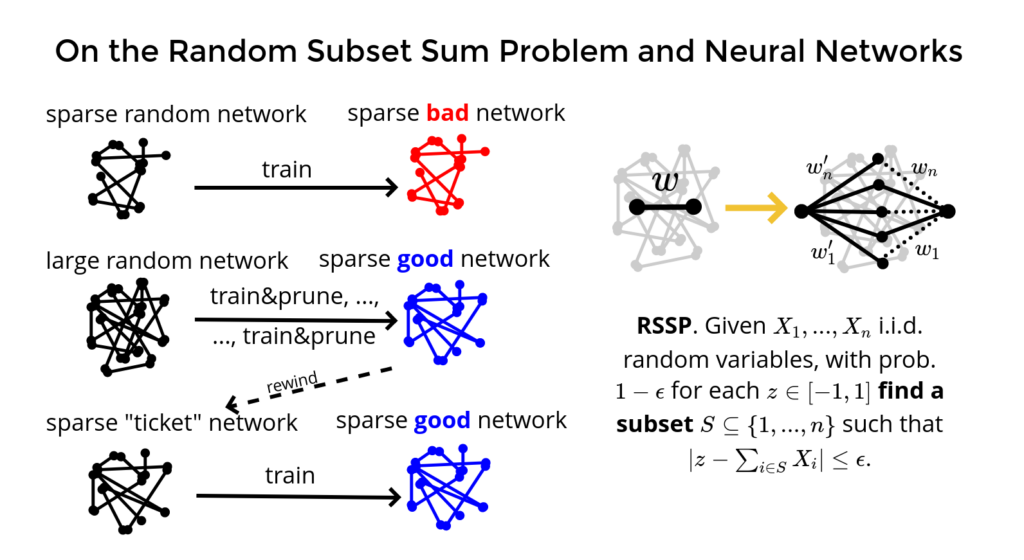
- Title: “On the Random Subset Sum Problem and Neural Networks”
- When: May 30, 2023 — 13:30
- Where: online seminar In’Tro
-
Abstract: The Random Subset Sum Problem (RSSP) is a fundamental problem in mathematical optimization, especially in understanding the statistical behavior of integer linear programs.
Recently, the theory related to this problem has also found applications in theoretical machine learning, providing key tools for proving the Strong Lottery Ticket Hypothesis (SLTH) for dense neural network architectures. In this talk, I will give a brief overview of this research direction and present my recent joint work that pushes the application of RSSP further by providing a proof of the SLTH for convolutional neural networks.
Hicham Lesfari recipient of the UniCA Foundation Award 2022
Hicham Lesfari, former PhD student of COATI supervised by Frédéric Giroire, is the recipient of the UniCA Foundation Award 2022, for his PhD thesis entitled Foundations of Networks towards AI (manuscript). Congratulations !
Foivos Fioravantes recipient of the 1st Computer Science Speciality Award 2022 of EDSTIC
Foivos Fioravantes, former PhD student of COATI supervised by Nicolas Nisse, is the recipient of the 1st Computer Science Speciality Award 2022 of EDSTIC, for his PhD thesis entitled Edge-labellings, vertex-colourings and combinatorial games on graphs (manuscript). Congratulations !
Un Palais de la Découverte des Sciences du numérique
Entretien avec Dorian Mazauric et Frédéric Havet sur le projet Terra Numerica pour le blog binaire du journal Le Monde.
PhD defense of Hicham Lesfari
- Title: “Foundations of Networks towards AI”
- When: October 7, 2022 — 9:00
- Where: Inria Sophia Antipolis, Euler violet
- Committee:
- Andrea Clementi, Full Professor, University of Rome Tor Vergata
- Romuald Elie, Research Scientist, DeepMind, Google
- Frédéric Giroire (supervisor), Directeur de recherche, CNRS
- Marc Lelarge (referee), Directeur de recherche, Inria Paris
- Pietro Michiardi (referee), Full Professor, EURECOM
- Giovanni Neglia, Directeur de recherche, Inria Sophia Antipolis
-
Abstract: The field of Artificial Intelligence (AI) has brought a broad impact on today’s society, leading to a gripping interaction between several scientific disciplines. In this respect, there has been a strong twofold interest across the literature. On the one hand, a growing trend in telecommunication networks consists in revisiting classic optimization problems using machine learning techniques in order to exploit their potential benefits. We focus on some challenges brought by the detection of anomalies in networks, and the allocation of resources within software-defined networking (SDN) and network function virtualization (NFV). On the other hand, a substantial effort has been devoted towards the theoretical understanding of the collective behavior of networks. We focus on some challenges brought by the study of majority dynamics within multi-agent systems, and the compression of artificial neural networks with the aim at increasing their efficiency. In this study, we contextualize the above focal points in the framework of investigating some foundations of networks; viewed through the lens of telecommunications networks and neural networks. We first focus our attention on developing graph similarity measures for network anomaly detection. Next, we study deterministic and stochastic majority dynamics in multi-agent systems. Then, we discuss the random subset sum problem in the context of neural network compression. Finally, we walk through some other miscellaneous problems.
- Titre: “Fondements Réseaux et IA”
-
Résumé: Le domaine de l’Intelligence Artificielle (IA) a un large impact sur la société d’aujourd’hui, ayant conduit notamment à une interaction passionnante entre plusieurs disciplines scientifiques. À cet égard, un double intérêt émerge dans la littérature. D’une part, une tendance croissante dans les réseaux de télécommunication consiste à revisiter les problèmes d’optimisation classiques en utilisant des techniques d’apprentissage automatique afin d’exploiter leurs avantages potentiels. Nous nous focaliserons sur certains défis posés par la détection d’anomalies dans les réseaux ainsi que l’allocation des ressources dans le cadre des réseaux logiciels (SDN) et de la virtualisation des fonctions réseau (NFV). D’autre part, un effort substantiel a été consacré dans le but d’apporter une compréhension théorique du comportement collectif des réseaux. Nous nous focaliserons sur certains défis posés par l’étude de la dynamique majoritaire au sein des systèmes multi-agents ainsi qu’à la compression des réseaux de neurones artificiels dans le but d’augmenter leur efficacité. Dans cette étude, nous contextualisons les points focaux ci-dessus dans le cadre de l’étude de certains fondements de réseaux; vus sous l’angle des réseaux de télécommunications et des réseaux neuronaux. Nous nous concentrons d’abord sur le développement de mesures de similarité de graphes pour la détection d’anomalies dans les réseaux. Ensuite, nous étudions la dynamique majoritaire déterministe et stochastique dans les systèmes multi-agents. Ensuite, nous discutons du problème de la somme de sous-ensembles aléatoires dans le contexte de la compression des réseaux neuronaux. Enfin, nous passons en revue quelques problèmes généraux divers.
On Computer Science Conferences and their Temporal Evolution

- Speaker: Pierluigi Crescenzi, GSSI, University of L’Aquila
- Title: On Computer Science Conferences and their Temporal Evolution — (watch the video)
- When: October 6, 2022 — 14:00
- Where: Campus SophiaTech, Forum F201, and online
-
Abstract: In this talk we will present the evolution of computer science conferences over the past 50 years, by analysing data from the DBLP database.
Our goal was to try and understand the evolution of each conference throughout its history, the ebb and flow in the popularity of its research areas, and the centrality of its authors, as measured by several metrics from network science, amongst other topics. In particular we tried to answer several different questions.
How did the conference evolve in terms of its number of authors, number of papers, and number of collaboration sizes? How much the conference was open to new entries? Did the percentage of female authors change over time? Were different topics more popular in different periods? If the conference covers a broad spectrum of research areas, did the percentage of each area change over time? Did the conference present the small-world phenomenon? What are the most influential authors of the conference?The tentative answer to these questions was given by either analysing only one conference at a time or by performing a comparative analysis between a specific set of conferences. We will also briefly present the web-based resources that accompany this talk. It goes without saying that our analysis has to be taken with a huge pinch of salt and is only meant to be food for thought for the community.
-
Short Bio: Pierluigi Crescenzi is a professor at the Gran Sasso Science Institute. Before joining GSSI, he has been researcher at the University of L’Aquila, and professor at the University of Rome, Florence, and Paris. He has taught in basically every field of computer science. He is the author of more than 130 scientific publications in the field of algorithm theory and its applications. He is co-author of 5 university textbooks, including 2 in English, and a popular Italian book. He is member of the editorial board of JCSS. He is co-author of the NP optimisation compendium, which is still widely cited. He is co-inventor of a US Patent on an IP address lookup algorithm and he has been a member of the steering committee of the COST 295 DYNAMO action. His current research is mostly focus on the analysis of complex networks and, more specifically, of temporal networks.
PhD defense of Foivos Fioravantes
- Title: “Edge-labellings, vertex-colourings and combinatorial games on graphs”
- When: September 26, 2022 — 14:00
- Where: Inria Sophia Antipolis, Euler violet
- Committee:
- Éric Sopena (referee), Professor, LaBRI, Université de Bordeaux
- Mariusz Woźniak (referee), Professor, AGH University of Science and Technology
- Julien Bensmail (supervisor), Associate professor, I3S, Université Côte d’Azur
- Nicolas Nisse (supervisor), Inria Research Officer, Inria Sophia Antipolis
- Théo Pierron, Associate professor, LIRIS, Université Claude Bernard Lyon 1
- Olivier Togni, Professor, LIB, Université de Bourgogne
-
Abstract: In this thesis, we consider two families of computational problems defined on graphs: proper edge-labellings and combinatorial games. We attack these problems in a similar (and classical) way: we show that they are computationally hard, and then find efficient algorithms for instances with specific structure.
First we focus on problems related to proper labellings of graphs. For some natural number k, a k-labelling is a weight function on the edges of a graph G, assigning weights, called labels in this context, from {1, . . . , k}. A k-labelling induces a vertex-colouring of G, where each vertex receives as colour the sum of the labels of its incident edges. A k-labelling is proper if the induced vertex-colouring is proper, i.e., such that any two adjacent vertices of G are assigned different colours. According to the so-called 1-2-3 Conjecture, any connected graph of order at least 3 should admit a proper 3-labelling. Weconsider three variations of this conjecture. We look into equitable proper k-labellings, for which the assigned labels appear an equal number of times. We then focus on proper labellings that also minimise the sum of labels being used, and finally, proper 3-labellings that also minimise the number of times that the label 3 is assigned.
The choice to study these variations is natural. Indeed, an equitable version of the 1-2-3 Conjecture claims that almost every graph G should admit an equitable proper 3-labelling. Also, the sum of labels of such a labelling would be at most 2|E(G)| and it would assign label 3 to at most one third of the edges of G. We prove that the introduced optimisation problems are NP-hard. Furthermore, through structural and algorithmical results, we propose new conjectures for the upper bounds of the parameters that we study, which we verify for specific graph classes (e.g. complete, bipartite, regular, 3-chromatic, etc.). Interestingly, our work gives further evidence that stronger variations of the 1-2-3 Conjecture could hold. We close our study of proper labellings by considering the problem of finding a largest induced subgraph of a given graph that admits a proper 1-labelling. This problem is proven to be computationally hard and not approximable within a ratio of O(|V(G)|^(1−c)) for every natural number c. Nevertheless, we provide efficient parameterised algorithms.In the second part of the thesis, we introduce and study the Maker-Breaker largest connected subgraph game. This game is played by two players, Alice and Bob, on a shared, initially uncoloured graph G. The two players take turns colouring the vertices of G, each one with their own colour, until there remains no uncoloured vertex. Alice is the winner of the game if, by the end, the largest connected subgraph of G induced by her colour is of order greater than k, where the natural number k is also given at the start of the game. Otherwise Bob wins the game. We also consider a Maker-Maker version of the same game, played in the same way, but in which the winner is the player whose colour induces the largest connected subgraph of G by the end of the game.
We first prove that deciding the outcome of both of these games is PSPACE-hard, and then proceed by providing efficient algorithms when the games are played on particular graph classes (e.g. paths, cycles, cographs, (q, q − 4)-graphs, etc.). Comparing the behaviour of these games, one of the main differences we observe is that Bob can never win the Maker-Maker version (if Alice plays optimally). Nevertheless, if Alice can win the Maker-Breaker version when playing on G for a value of k equal to half the order of G (the best outcome she can hope for), then she can build a connected subgraph of the same order for the Maker-Maker version; such graphs are called A-perfect. We then study regular graphs that are A-perfect and prove that any 3-regular A-perfect graph has order at most 16. We finish by providing sufficient conditions for a graph to be A-perfect. - Titre: “Étiquetages d’arêtes, colorations de sommets et jeux combinatoires sur les graphes”
-
Résumé: Cette thèse considère deux familles de problèmes définis sur des graphes : les étiquetages d’arêtes propres et les jeux combinatoires. Nous traitons ces problèmes de façon similaire (et classique) : nous montrons que les problèmes considérés sont difficiles à résoudre, puis nous trouvons des algorithmes efficaces sur des instances restreintes.
Nous nous concentrons d’abord sur des problèmes concernant des étiquetages propres de graphes. Pour un entier k fixé, un k-étiquetage d’un graphe G est une fonction associant à chaque arête de G une étiquette parmi {1, . . . , k}. Un k-étiquetage induit une coloration des sommets de G, où chaque sommet reçoit comme couleur la somme des étiquettes de ses arêtes incidentes. Un k-étiquetage est propre si, dans la coloration induite, deux sommets adjacents de G reçoivent des couleurs différentes. D’après la Conjecture 1-2-3, tout graphe connexe d’ordre au moins 3 admet un 3-étiquetage propre. Nous considérons trois variantes de cette conjecture. Nous étudions les k-étiquetages propres équilibrés, pour lesquels les étiquettes assignées apparaissent dans les mêmes proportions.
La deuxième variante concerne les étiquetages propres qui minimisent la somme des étiquettes utilisées. Enfin, nous nous intéressons aux 3-étiquetages propres qui minimisent le nombre de fois où l’étiquette 3 est attribuée. Le choix d’étudier ces variantes est naturel. En effet, une version équilibrée de la Conjecture 1-2-3 est que presque tous les graphes G admettent un 3-étiquetage propre équilibré. En outre, la somme des étiquettes d’un tel étiquetage est au plus égale à 2|E(G)| et associe l’étiquette 3 à au plus un tiers des arêtes de G. Nous prouvons que les problèmes d’optimisation introduits sont NP-difficiles. Grâce à des résultats structurels et algorithmiques, nous sommes amenés à proposer de nouvelles conjectures pour ces problèmes, que nous vérifions sur quelques classes de graphes (complets, bipartis, réguliers, 3-chromatiques, etc.).
Notre travail renforce l’idée que des variantes plus fortes de la Conjecture 1-2-3 pourraient être vraies. Nous terminons en considérant le problème consistant à trouver un plus grand sous-graphe induit d’un graphe donné qui admet un 1-étiquetage propre. Il est prouvé que ce problème est difficile à résoudre et qu’il n’est pas approximable à un facteur O(|V (G)|^(1−c)) près pour tout entier c. Néanmoins, nous fournissons des algorithmes paramétrés efficaces.La deuxième partie de la thèse introduit le jeu du plus grand sous-graphe connexe Maker-Breaker, joué par deux joueurs, Alice et Bob, sur un graphe G, initialement non coloré. Les joueurs colorent à tour de rôle les sommets de G, chacun avec sa couleur, jusqu’à ce que tous les sommets soient colorés. Alice est la gagnante si, à la fin, le plus grand sous-graphe connexe de G induit par sa couleur est d’ordre au moins k, un entier fixé. Sinon, Bob gagne le jeu. Nous considérons aussi une version Maker-Maker du même jeu, dans laquelle le gagnant est le joueur dont la couleur induit le plus grand sous-graphe connexe de G à la fin du jeu. Nous prouvons que décider de l’issue de ces deux jeux est PSPACE-difficile et nous fournissons des algorithmes efficaces pour le cas où le jeu se déroule dans certaines familles de graphes (chemins, cycles, cographes, (q,q−4)-graphes, etc.).
En comparant ces deux jeux, la principale différence que nous observons est que Bob ne peut jamais gagner la version Maker-Maker (si Alice joue de manière optimale). Pour une valeur de k égale à la moitié de l’ordre de G, remarquons que si Alice peut gagner la version Maker-Breaker alors elle peut aussi construire un sous-graphe connexe du même ordre dans la version Maker-Maker ; de tels graphes sont nommés A-parfaits. Nous étudions les graphes réguliers qui sont A-parfaits et prouvons que tout graphe 3-régulier A-parfait a au plus 16 sommets. Nous terminons en fournissant des conditions suffisantes pour qu’un graphe soit A-parfait.
GRASTA 2022
10th Workshop on GRAph Searching, Theory and Applications (GRASTA 2022)
- When: May 16-20, 2022
- Where: Porquerolles, France
- Contact: Nicolas Nisse (organizing chair)
- Link: conference website
Best paper award
The paper On Finding k Earliest Arrival Time Journeys in Public Transit Networks [1] won the best paper award at ICORES 2022.
Congratulation to the authors!
The source code used to conduct experiments for this paper is here.
- A. Al-Zoobi, D. Coudert, A. Finkelstein, and J. Régin, “On Finding k Earliest Arrival Time Journeys in Public Transit Networks,” in 11th International Conference on Operations Research and Enterprise Systems (ICORES), Virtual event, France, 2022, pp. 314-325.
[BibTeX] [Download PDF]@inproceedings{alzoobi:hal-03559992, TITLE = {{On Finding k Earliest Arrival Time Journeys in Public Transit Networks}}, AUTHOR = {Al-Zoobi, Ali and Coudert, David and Finkelstein, Arthur and R{\'e}gin, Jean-Charles}, URL = {https://hal.inria.fr/hal-03559992}, BOOKTITLE = {{11th International Conference on Operations Research and Enterprise Systems (ICORES)}}, ADDRESS = {Virtual event, France}, PAGES = {314-325}, YEAR = {2022}, MONTH = Feb, KEYWORDS = {Public Transit Routing ; shortest path ; dissimilar paths}, PDF = {https://hal.inria.fr/hal-03559992/file/ptkssp.pdf}, HAL_ID = {hal-03559992}, HAL_VERSION = {v1}, }