The following upstream research items are useful for the applications we work on.
- Diffusion process in gaseous mixtures
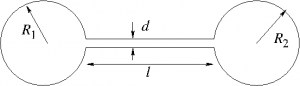Duncan and Toor’s experiment device
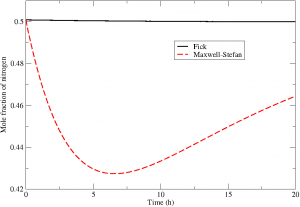
Fick’s law is the standard model for gaseous diffusion, including air. Duncan and Toor pointed out that the Fickian diffusion was not enough to tackle some multi-species situations when each component of the mixture has differents scales of friction properties. In particular, in this experiment, the nitrogen concentration is equal in both bulbs of the device. Fick’s law states that nitrogen does not move, whereas, physically, it does move. In fact, Maxwell-Stefan’s equations allow to give the real behavior of each species and can be used for further studies involving an helium-oxygen mixture in the airways.
Mole fraction of nitrogen computed thanks to Fick’s law or Maxwell-Stefan’s equations
- Fluid/kinetic coupling
The mathematical modeling used to describe the behavior of aerosols (or sprays) in the airway of the lung is based on a fluid/kinetic point of view. The fluid is described via the classical equations of fluid mechanics (Navier-Stokes equations for instance), whereas the whole set of particle is described thanks to one single Vlasov-type equation, prescribing of the evolution the particle density function. The interaction is two-way: the fluid accelerates the particles through the drag force, and the aerosol produces back a retroaction force applied on the fluid.
- Inverse Problems
We are interested in the derivation of stability estimates for the parameters of our models: for instance the bistable equation modeling a front propagation or the Stokes system. In particular, we consider the Stokes system completed with mixed Neumann and Robin boundary conditions and we want to recover the Robin coefficient (and obtain stability estimate for it) from measurements available on a part of the boundary where Neumann conditions are prescribed. These type of system appear in blood flow as well as air flow modelling.
Based on local Carleman inequalities, we prove Holder and logarithmic stability estimates associated to the unique continuation property for the Stokes system. For the identification parameter problem, we obtain a logarithmic stability estimate.
This page is in progress
