This project is published on Computer Graphics Forum and was presented at EUROGRAPHICS Symposium on Geometry Processing 2013 where it was given the 2nd Best Paper Award.
Authors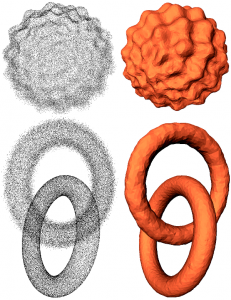
Simon Giraudot, David Cohen-Steiner & Pierre Alliez
Abstract
We propose a noise-adaptive shape reconstruction method specialized to smooth, closed shapes. Our algorithm takes as input a defect-laden point set with variable noise and outliers, and comprises three main steps. First, we compute a novel noise-adaptive distance function to the inferred shape, which relies on the assumption that the inferred shape is a smooth submanifold of known dimension. Second, we estimate the sign and confidence of the function at a set of seed points, through minimizing a quadratic energy expressed on the edges of a uniform random graph. Third, we compute a signed implicit function through a random walker approach with soft constraints chosen as the most confident seed points computed in previous step.




