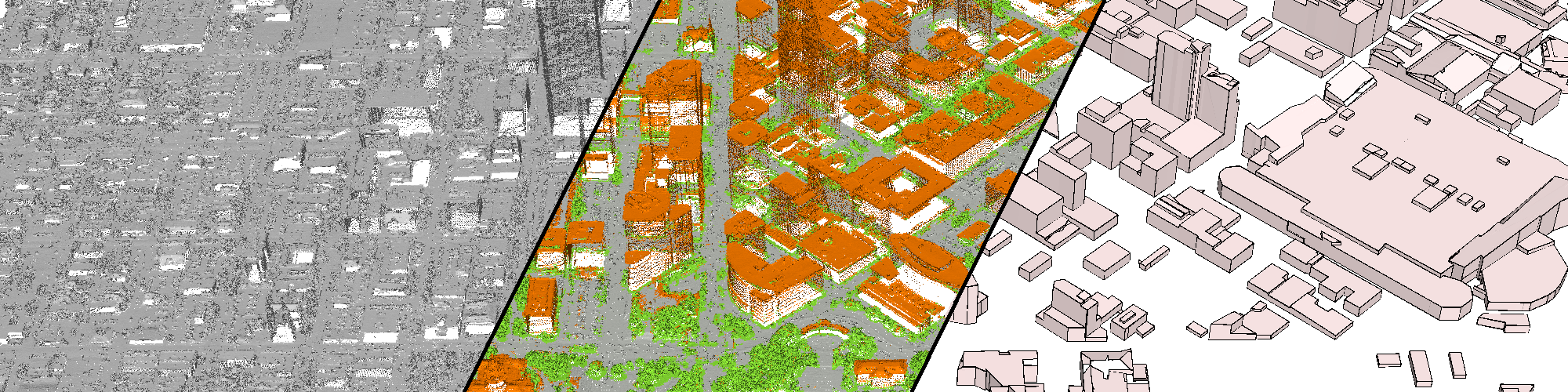
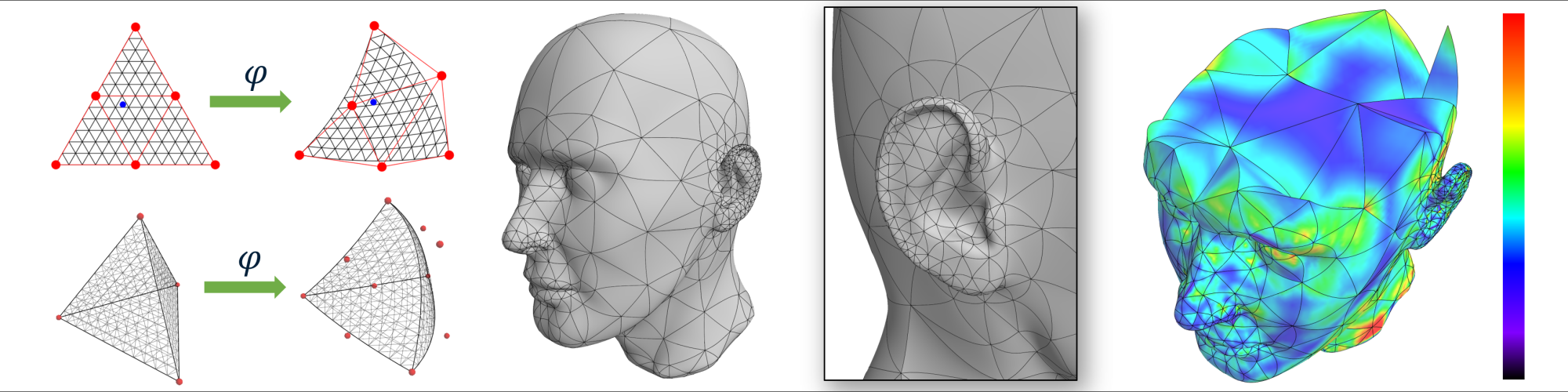
Welcome to the TITANE group at Inria!
Our research activities focus on geometric modeling and processing, on remote sensing, and on related areas such as image processing and computer vision.
Our overall objective is the computerized geometric modeling of complex scenes from physical measurements. On the geometric modeling and processing pipeline, this objective corresponds to steps required for conversion from physical to effective digital representations: analysis, reconstruction and approximation.
News
• Accepted paper at CVPR 2022 on good configurations of primitives on 3D point clouds.
• Accepted paper at CGF 2022 on simplification of 2D polygonal partitions.
• Accepted paper at ACM SIGGRAPH 2022 on alpha wrapping .
• Accepted paper at CGF 2022 on simplification of 2D polygonal partitions.
• Accepted paper at ACM SIGGRAPH 2022 on alpha wrapping .
Keywords
Geometric modeling, geometry processing, remote sensing, image analysis, computational geometry, surface reconstruction, geometry compression, mesh generation, machine learning.
