ERC Starting Grant IRON (Robust Geometry Processing) 2011 – 2016
Principal Investigator: Pierre Alliez, INRIA Sophia Antipolis – Mediterranee
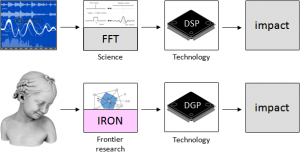
Short Summary: The purpose of this project is to bring forth the full scientific and technological potential of Digital Geometry Processing by consolidating its most foundational aspects. Our methodology will draw from and bridge the two main communities (computer graphics and computational geometry) involved in discrete geometry to derive algorithmic and theoretical contributions that provide both robustness to noisy, unprocessed inputs, and strong guarantees on the outputs. The intended impact is to make the digital geometry pipeline as generic and ironclad as its Digital Signal Processing counterpart.
Scientific Context
Digital geometry processing (DGP) is a now a core scientific field seeking to develop automated methods in order to deal with the ever-increasing variety and abundance of geometric data. The grand challenge for DGP is to elaborate the theoretical and algorithmic foundations for the acquisition, manipulation, transmission and manufacturing of complex 3D objects.
A major driving force in the field in recent years has been to elaborate mathematical and algorithmic foundations for analyzing and processing complex shapes, the analogue of analyzing and filtering signals in digital signal processing (DSP). The main results are discrete equivalents of basic notions and methods of differential geometry, such as curvature and shape fairing of polyhedral surfaces. Another major drive, of central importance in this proposal, has been to create methods for geometry reconstruction and approximation, the analogue of measuring and converting signals in DSP. The challenge is considerably more difficult than for ordinary signals due to the variety of geometric data. Among the many approaches proposed, the ones which are theoretically-founded are able to prove correctness of their reconstructions and approximations with respect to the geometry and topology of the inferred or input shapes. Furthermore, reliable implementations of these methods have been made possible through the introduction of new paradigms for reliable geometric computing. For computational geometers correctness and reliability are considered the two foremost issues, but the methods proposed thus far typically assume ideal, computer-synthesized data. These assumptions on input data (such as regular, isotropic, or noise-free sampling) clash with the practical reality in which datasets acquired from the physical world are imperfect and irregularly spaced.
Geometric data are increasingly acquired through measurements from scanners, satellites, ultrasound, etc. These sources of data are reputedly unfit for direct processing: they are typically ridden with noise, non-uniform sampling, and even outliers. In addition, geometric datasets are increasingly obtained from a variety of acquisition systems, making them heterogeneous as well. Moreover, current processing tools throughout the geometry pipeline can make the data worse as they involve conversions and alterations that commonly induce foldovers and self-intersections for surfaces, badly-shaped elements and erroneous topology for volumes, etc.
Dire Needs
While existing DGP algorithms have been successfully demonstrated on select datasets, their lack of industrial-strength robustness to imperfect and heterogeneous geometric datasets severely impairs their use in industrial applications. For this very reason we have seen in recent years some work devoted to the repair of defect-laden data and a number of preliminary approaches to deal with imperfect datasets. The initial grand promise of DGP as a successful extension to DSP (i.e., as robust and general as DSP) for the very special “signals” that shapes are has not been realized yet. The tenet of this proposal is that the potential of geometry processing techniques is far from being reached, and that to realize its full potential, one must tenaciously address the most enduring and fundamental problems hampering resilience to imperfect and heterogeneous input:
• Need for robustness. The vast majority of geometry processing methods only function for idealized, defect-free input data such as point sets without outliers, or intersection–free 2–manifold (surface) triangle meshes—not raw polygon soups. For instance, although many surface reconstruction algorithms from point sets are fairly robust to noise, considerably fewer techniques are simultaneously robust to highly non-uniform sampling, noise and outliers. Similarly, almost none of the mesh processing algorithms of the “standard geometry processing toolbox” are robust to polygon soups. Robustness to defect-laden inputs is a largely unaddressed scientific challenge, and we argue that there is a need for a unified theory and algorithms capable of dealing with these data hampered with a variety of imperfections.
• Need for genericity. Nearly all current geometry processing methods are specialized to point sets, triangle meshes, or contours, but cannot handle mixed inputs. When we need to deal with heterogeneous data or with new data types, the current solution consists of converting them to a common representation or to devise yet another specialized method. As each conversion adds some geometric inaccuracy and possibly some defects as well, this solution can be even more damaging when used as an input to non-robust algorithms. Instead of requesting the practitioner to systematically convert everything, there is a need for a unified way of dealing with heterogeneous data.
• Need for guarantees. The majority of geometry processing algorithms do not provide guarantees for their outputs, most likely because many target applications in computer graphics care about visual impact more than practical guarantees. Computational geometers, however, have considered guarantees a priority. Alas, the theoretical assumptions on the input data are often not met in practical applications. For example, the provably correct Delaunay-based surface reconstruction algorithms assume an epsilon sampling (i.e., dense and isotropic). Other algorithms provide guarantees without unattainable assumptions, but do not fully address the problem. One concrete example is a recent mesh refinement algorithm which guarantees intersection-free and geometric error tolerances, but generates isotropic meshes that are unnecessarily large.
• Need for automation. The lack of robustness, genericity, and guarantees we mentioned above conspire to make the task of streamlining the whole processing pipeline almost impossible: while each algorithm along the pipeline is presented as a fully automatic process in academic papers, their requirements for inputs and lacks of guarantees on outputs prevent these building blocks from working together seamlessly. For instance, an aircraft manufacturer who needs to perform computational fluid dynamics simulation on the CAD model of a helicopter will have to first convert the model into a surface mesh that is watertight and intersection-free. This seemingly simple process currently takes weeks for an experienced engineer, as repair and defeaturing of the converted mesh requires trial and error. However, the final simulation takes only one hour of parallel computation on a cluster of 2K computers. As this procedure must be repeated for each major editing of the CAD model, and as it is the wall clock time of a process that matters in such industrial applications, it is of crucial important to reduce, through automation, the conversion duration from weeks to hours.
People
• Pierre Alliez (principal investigator) January 2011 – today
• Kaimo Hu (postdoctoral fellow on remeshing) – Sep 2012 – August 2013
• Manish Mandad (Ph.D. student on robust shape approximation) – Nov 2012 – today
• Yiyi Wei (postdoctoral fellow on well-centered triangulations) – May 2012 – October 2012
• David Bommes (postdoctoral fellow on surface and domain tiling) – May 2012 – today
• Manish Mandad (master intern on robust shape approximation, then Ph.D. student) – May 2012 – today
• Florent Lafarge (Inria researcher) – December 2011 – today
• Simon Giraudot (Ph.D. student on robust shape reconstruction) – November 2011 – today
• Sagar Chordia (intern from IIT Bombay on shape approximation with guarantees) – May-July 2011
• Julie Digne (postdoctoral fellow on robust piecewise smooth surface reconstruction) – May 2011 – August 2012
• Renata Nascimento (visiting Ph.D. student from PUC, Rio de Janeiro on coarse quadrangle surface tiling) – September 2011 – March 2012
• Paul Seron (master intern on reconstruction of urban scenes) – April-September 2011
Visits to Inria
2013:
• Henrik Zimmer (RWTH Aachen) – July
• David Salinas (Grenoble University) – May
2012:
• Prof. Leif Kobbelt (RWTH Aachen) – one week during October
• Prof. Mathieu Desbrun (Caltech) – one week during July
• Prof. Alla Sheffer (UBC) – one week during June
2011:
• David Bommes (Ph.D. student from RWTH Aachen, Germany) – one week during June
• Prof. Alla Sheffer (UBC, Canada) – two weeks during March-April
• Thijs van Lankveld (Ph.D. student at the University of Utrecht, the Netherland) – one week during March
Visits from Inria
2015:
• Pierre Alliez and Manish Mandad visited RWTH (Prof. Kobbelt) – 2 weeks during February
2013:
• David Bommes visited Caltech (the Applied Geometry group and Multi-Res Modeling group) – 4 weeks from May
2012:
• Pierre Alliez visited RWTH (Prof. Kobbelt) – during October
2011:
• Pierre Alliez visited Caltech (the Applied Geometry group) – one month during October
• Julie Digne visited Caltech (the Applied Geometry group) – 5 weeks during October
Conferences
2013:
• Pierre Alliez, Florent Lafarge and David Bommes, EUROGRAPHICS conference, Girona.
• Pierre Alliez, Simon Giraudot, and Manish Mandad, EUROGRAPHICS Symposium on Geometry Processing, Genova.
• Pierre Alliez, Workeshop on Computational Electrostatics for Biological Applications 2013.
2012:
• Pierre Alliez, Julie Digne and Simon Giraudot, workshop on new Trends in Applied Geometry, Gazzada, February.
• Julie Digne and Florent Lafarge, 25th Conference on Computer Vision and Pattern Recognition, Providence, June.
• David Bommes, EUROGRAPHICS annual conference, Cagliari, May.
2011:
• Pierre Alliez, Oberwolfach workshop on Trends in Mathematical Imaging and Surface Processing, February.
• Pierre Alliez and Julie Digne, EUROGRAPHICS Symposium on Geometry Processing.
• Pierre Alliez, Trimester Program on Computational Manifolds and Applications, Rio de Janeiro.
Invited talks
2013:
• Pierre Alliez, invited speaker at CEBA 2013 (Genova)
2012:
• Julie Digne, invited speaker at Mathematics and Image Analysis (January, Paris)
• Pierre Alliez, invited speaker, Advances in Architectural Geometry (September, Paris).
• Pierre Alliez, invited speaker at the MICCAI workshop on Mesh Processing in Medical Image Analysis (October, Nice).
• Pierre Alliez, invited speaker at 3DIMPVT: 3D Imaging, Modeling, Processing, Visualization and Transmission (October, Zurich).
Events
2013:
• David Bommes has received the EUROGRAPHICS thesis award.
2012:
• Florent Lafarge is organizing the International Workshop on Point Cloud Processing in conjunction with CVPR 2012:
• Julie Digne is giving a course on point sets and surfaces at the graduate school of the EUROGRAPHICS Symposium on Geometry Processing.
• Pierre Alliez is giving a course on the CGAL library at the graduate school of the EUROGRAPHICS Symposium on Geometry Processing.
Publications / posters / presentations
- Structure-Aware Mesh Decimation
David Salinas, Florent Lafarge and Pierre Alliez.
Computer Graphics Forum, Wiley-Blackwell 2015. - A Surface Reconstruction Method for In-Detail Underwater 3D Optical Mapping
Ricard Campos, Rafael Garcia, Pierre Alliez and Mariette Yvinec.
International Journal of Robotics Research, SAGE Publications (UK and US), 2015. - LOD Generation for Urban Scenes
Yannick Verdie, Florent Lafarge and Pierre Alliez.
ACM Transactions on Graphics, Association for Computing Machinery, 2015. - Anti-Cropping Blind Resynchronization for 3D Watermarking
Rolland-Nevière Xavier, Gwenaël Doërr and Pierre Alliez.
IEEE International Conference on Acoustic, Speech Signal Processing 2015. - Triangle Surface Mesh Watermarking based on a Constrained Optimization Framework
Rolland-Nevière Xavier, Gwenaël Doërr and Pierre Alliez.
IEEE Transactions on Information Forensics and Security 2014. - CGALmesh: a Generic Framework for Delaunay Mesh Generation
Clément Jamin, Pierre Alliez, Mariette Yvinec and Jean-Daniel Boissonnat.
ACM Transactions on Mathematical Software, Association for Computing Machinery, 2014. - Indoor Scene Reconstruction using Feature Sensitive Primitive Extraction and Graph-cut
Sven Oesau, Florent Lafarge and Pierre Alliez.
ISPRS Journal of Photogrammetry and Remote Sensing, Elsevier, 2014. - Level-of-Detail Quad Meshing
Hans-Christian Ebke, Marcel Campen, David Bommes and Leif Kobbelt.
Association for Computing Machinery (ACM), 2014. - Detecting parametric objects in large scenes by Monte Carlo sampling
Yannick Verdie and Florent Lafarge.
International Journal of Computer Vision, Springer Verlag, 2014. - Zometool Shape Approximation
Henrik Zimmer, Florent Lafarge, Pierre Alliez and Leif Kobbelt.
Geometric Modeling and Processing 2014. - Spread Transform and Roughness-based Shaping to Improve 3D Watermarking based on Quadratic Programming
Rolland-Nevière Xavier, Gwenaël Doërr and Pierre Alliez.
IEEE International Conference on Image Processing 2014. - Robust Shape Reconstruction and Optimal Transportation
Pierre Alliez, Simon Giraudot and David Cohen-Steiner.
Courbure discrète : théorie et applications 2014. - State of the Art in Surface Reconstruction from Point Clouds
Matthew Berger, Andrea Tagliasacchi, Lee Seversky, Pierre Alliez, Joshua Levine, Andrei Sharf and Claudio Silva.
Eurographics 2014 – State of the Art Reports. - Special issue of Graphical Models.
Pierre Alliez, Ying He and Yongjie Zhang.
Geometric Modeling and Processing 2014. - CGALmesh: a Generic Framework for Delaunay Mesh Generation
Cl ́ement Jamin, Pierre Alliez, Mariette Yvinec and Jean-Daniel Boissonnat.
INRIA Research Report 2014. - Robust diameter-based thickness estimation of 3D objects
Rolland-Nevière Xavier, Gwenaël Doërr and Pierre Alliez.
Graphical Models, Elsevier, 2013. - Splat-based Surface Reconstruction from Defect-Laden Point Sets
Ricard Campos, Rafael Garcia, Pierre Alliez and Mariette Yvinec.
Graphical Models, Elsevier, 2013. - Quad-Mesh Generation and Processing: A Survey
David Bommes, Bruno Lévy, Nico Pietroni, Enrico Puppo, Claudio Silva, Marco Tarini and Denis Zorin.
Computer Graphics Forum. - QEx: Robust Quad Mesh Extraction
Michael Kremer, David Bommes, Isaak Lim and Leif Kobbelt.
SIGGRAPH Asia 2013. - Advanced Automatic Hexahedral Mesh Generation from Surface Quad Meshes
Hans-Christian Ebke, David Bommes, Marcel Campen and Leif Kobbelt.
International Meshing Roundtable 2013. - Indoor Scene Reconstruction using Primitive-driven Space Partitioning and Graph-cut
Sven Oesau, Florent Lafarge and Pierre Alliez.
Eurographics Workshop on Urban Data Modelling and Visualisation 2013. - Noise-Adaptive Shape Reconstruction from Raw Point Sets
Simon Giraudot, Pierre Alliez and David Cohen-Steiner.
To appear at EUROGRAPHICS Symposium on Geometry Processing (SGP) 2013. - Integer-Grid Maps for Reliable Quad Meshing
David Bommes, Marcel Campen, Hans-Christian Ebke, Pierre Alliez, Leif Kobbelt.
To appear at SIGGRAPH 2013. - On the Equilibrium of Simplicial Masonry Structures
Fernando de Goes, Pierre Alliez, Houman Owhadi and Mathieu Desbrun.
To appear at SIGGRAPH 2013. - Surface Reconstruction through Point Set Structuring.
Florent Lafarge and Pierre Alliez.
EUROGAPHICS 2013. - Anisotropic Rectangular Metric for Polygonal Surface Remeshing
Bertrand Pellenard, Jean-Marie Morvan and Pierre Alliez.
International Meshing Roundtable 2012 - Feature-Preserving Surface Reconstruction and Simplification from Defect-Laden Point Sets.
Julie Digne, David Cohen-Steiner, Pierre Alliez, Mathieu Desbrun, Fernando de Goes.
Journal of Mathematical Imaging and Vision. - An Optimal Transport Approach to Robust Reconstruction and Simplification of 2D Shapes.
Fernando de Goes, David Cohen-Steiner, Pierre Alliez, and Mathieu Desbrun.
Symposium on Geometry Processing, 2011. - Isotropic 2D Quadrangle Meshing with Size and Orientation Control.
Bertrand Pellenard, Pierre Alliez and Jean-Marie Morvan.
International Meshing Roundtable 2011.
Bertand Pellenard also presented a poster which won the best technical poster award. - Progressive Compression of Manifold Polygon Meshes.
Adrien Maglo, Clément Courbet, Pierre Alliez and Céline Hudelot.
Proceedings of Shape Modeling International 2012. - Efficient Monte Carlo Sampler for Detecting Parametric Objects in Large Scenes.
Yannick Verdie and Florent Lafarge.
Proceeding of European Conference on Computer Vision (ECCV), 2012. - Similarity based filtering of point clouds.
Julie Digne.
Proceedings of 25th Conference on Computer Vision and Pattern Recognition (International Workshop on Point Cloud Processing) 2012. - Feature-Preserving Surface Reconstruction and Simplification from Defect-Laden Point Sets.
Julie Digne, David Cohen-Steiner, Pierre Alliez, Mathieu Desbrun, Fernando de Goes.
INRIA Research Report 7991, June 2012. - Anisotropic Surface Tiling.
Bertrand Pellenard, Pierre Alliez and Jean-Marie Morvan.
Poster at EUROGRAPHICS Symposium on Geometry Processing 2012. - Scale space meshing of raw data point sets.
Julie Digne.
Oral presentation at EUROGRAPHICS Symposium on Geometry Processing 2012. - Anisotropic Rectangle Metric for Surface Tiling.
Bertrand Pellenard, Pierre Alliez and Jean-Marie Morvan.
Curves and Surfaces 2012.