PySAP-MRI: a Python Package for MR Image Reconstruction
Full text in HAL (see exact reference [1] below)
We present the open-source MRI plugin, called pysap-mri, of the software package PySAP (Python Sparse data Analysis Package). PySAP offers a large set of fast wavelet transforms and a range of integrated optimization algorithms in Python. Pysap-mri is aimed at researchers who need fast MR image reconstruction algorithms for under-sampled k-space data. This plugin provides methods, tools and examples for MR image reconstruction in various acquisition setups (2D and 3D imaging, Cartesian and non-Cartesian readout, parallel imaging, etc.) in the context of accelerated acquisitions using compressed sensing. This plugin is available on Pypi as pysap-mri 0.1.1.
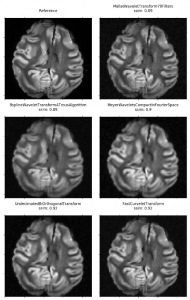
Top: Reference MR baboon image (left) and reconstructed image using Mallat WT. Center: MR images reconstructed image B-spline and Meyer WT. Bottom: MR images solutions computed using the analysis-based formulation and tight frames. The SSIM scores appear on top of each panel.
Analysis vs Synthesis-based Regularization for combined Compressed Sensing and Parallel MRI Reconstruction at 7 Tesla.
Full text in HAL (see exact reference [2] below)
Compressed Sensing (CS) has allowed a significant reduction of acquisition times in MRI, especially in the high spatial resolution (e.g., 400 µm) context. Nonlinear CS reconstruction usually relies on analysis (e.g., Total Variation) or synthesis (e.g., wavelet) based priors and L1 regularization to promote sparsity in the transform domain. Here, we compare the performance of several orthogonal wavelet transforms with those of tight frames for MR image reconstruction in the CS setting combined with parallel imaging (multiple receiver coil). We show that overcomplete dictionaries such as the fast curvelet transform provide improved image quality as compared to orthogonal transforms. For doing so, we rely on an analysis-based formulation where the underlying L1 regularized criterion is minimized using a primal dual splitting method (e.g., Condat-Vu algorithm). Validation is performed on ex-vivo baboon brain T2* MRI data collected at 7 Tesla and restrospectively under-sampled using non-Cartesian schemes (radial and Sparkling). We show that multiscale analysis priors based on tight frames instead of orthogonal transforms achieve better image quality (pSNR, SSIM) in particular at low signal-to-noise ratio.
Self-calibrating nonlinear reconstruction algorithms for variable density sampling and parallel reception MRI.
Full text in HAL (see exact reference [3] below)
Compressed Sensing must be combined in high resolution with parallel reception as multichannel coil acquisitions maintain high input signal-to-noise ratio (SNR). To get rid of usual parallel imaging limitations (output SNR loss), non-Cartesian trajectories provide a gain in sampling efficiency in the CS context. In this paper, we propose a self-calibrating MRI reconstruction framework that handles variable density sampling. Low resolution sensitivity maps are estimated from the low frequency k-space content using an original and fast method while MR images are reconstructed using a nonlinear iterative algorithm, which promotes sparsity in the wavelet domain. As regards the optimization task, we compare three first-order proximal gradient methods (FB, FISTA, POGM) and evaluate their respective convergence speed. Comparison with state-of-the-art (i.e., 1-ESPIRiT) suggests that our self-calibrating POGM-based algorithm outperforms current approaches both in terms of image quality and computing time on prospectively accelerated ex-vivo and in-vivo data collected at 7 Tesla and we will focus more specifically on prospective non-Cartesian 8-fold accelerated in vivo Human brain data.
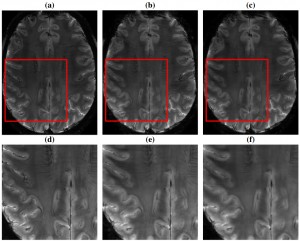
(a) Cartesian reference, (b) Self-calibrating POGM-based and (c) L1-ESPIRiT reconstructions from 8-fold accelerated prospective CS based on Sparkling trajectories. (d)-(f) respective zooms in the red square.
Calibration-less parallel imaging compressed sensing reconstruction based on OSCAR regularization
Full text in HAL (see exact reference [4] below)
Over the last decade, the combination of parallel imaging (PI) and compressed sensing (CS) in magnetic resonance imaging (MRI) has allowed to speed up acquisition while maintaining a good signal-to-noise ratio (SNR) for millimetric resolution. Self-calibrating techniques such as L1-ESPiRIT have emerged as a standard approach to estimate the coil sensitivity maps that are required at the reconstruction stage. Although straightforward in Cartesian acquisitions, these approaches become more computationally demanding in non-Cartesian scenarios especially for high resolution imaging (e.g. 500 µm in plane). Instead, calibration-less techniques no longer require this prior knowledge to perform multi-channel image reconstruction from undersampled k-space data. In this work, we introduce a new calibration-less PI-CS reconstruction method that is particularly suited to non-Cartesian data. It leverages structure sparsity of the multi-channel images in a wavelet transform domain while adapting to SNR inhomogeneities across receivers thanks to the OSCAR-norm regularization. Comparison and validation on 8 to 20-fold prospectively accelerated high-resolution ex-vivo human brain MRI data collected at 7 Tesla shows that the subbandwise OSCAR-norm regularization achieves the best trade-off between image quality and computational cost at the reconstructions stage compared to other tested versions (global, scalewise and pixel-wise). This approach provides slight to moderate improvement over its state-of-the-art competitors (self-calibrating 1-ESPIRiT method and calibration-less AC-LORAKS and CaLM methods) in terms of closeness to the Cartesian reference magnitude image. Importantly, it also preserves much better phase information compared to other approaches.
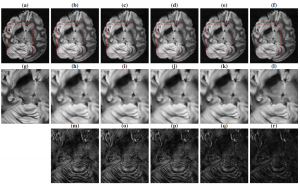
(a) Cartesian reference. (b) Reconstruction with no regularization term. (c) Reconstruction based on the group-LASSO penalty. (d) Reconstruction based on the sparse group-LASSO penalty. (e) Reconstruction based on OSCAR penalty. (f) Reconstruction based on L1-ESPIRiT. (g)-(l) Respective zooms in the red square, (m)-(r) zoom of the difference between the Cartesian reference and the reconstructed image.
Online MR image reconstruction for compressed sensing acquisition in T2* imaging
Full text in HAL (see exact reference [5] below)
Reducing acquisition time is a major challenge in high-resolution MRI that has been successfully addressed by Compressed Sensing (CS) theory. While the scan time has been massively accelerated by a factor up to 20 in 2D imaging, the complexity of image recovery algorithms has strongly increased, resulting in slower reconstruction processes. In this work we propose an online approach to shorten image reconstruction times in the CS setting. We leverage the segmented acquisition in multiple shots of k-space data to interleave the MR acquisition and image reconstruction steps. This approach is particularly appealing for 2D high-resolution T2*-weighted anatomical imaging as the largest timing interval (i.e. Time of Repetition) between consecutive shots arises for this kind of imaging. During the scan, acquired shots are stacked together to form mini-batches and image reconstruction may start from incomplete data. For each newly available mini-batch, the previous partial solution is used as warm restart for the next sub-problem to be solved in a timing window compatible with the given TR and the number of shots stacked in a mini-batch.
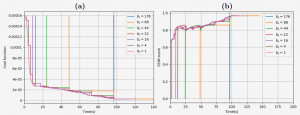
Single-channel retrospective Cartesian reconstruction: (a) evolution over time of cost function and of (b) the SSIM score for different batch sizes bs. The dark dashed line marks the end of acquisition.
We demonstrate the interest and time savings of using online MR image reconstruction for Cartesian and non-Cartesian sampling strategies combined with a single receiver coil. Next, we extend the online formalism to address the more general multi-receiver phased array acquisition scenario. In this setting, calibrationless image reconstruction is adopted to remain compatible with the timing constraints of online delivery. Our retrospective and prospective results on ex-vivo 2D T2*-weighted brain imaging show that high-quality MR images are recovered by the end of acquisition for single receiver acquisition and that additional iterations are required when parallel imaging is adopted. Overall, our approach implemented through the Gadgetron framework may be compatible with the data workflow on the scanner to provide the physician with reliable MR images for diagnostic purposes.
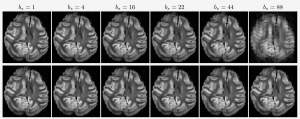
Online reconstruction of 15-fold (S=34 shots) retrospectively accelerated Cartesian scan of ex vivo baboon brain in a single-channel coil acquisition setup. Images reconstructed for increasing values of mini-batch size bs at the end of acquisition (top) and at convergence (bottom).
References
[1] El Gueddari L, GR C, Ramzi Z, Farrens S, Starck S, et al.. PySAP-MRI: a Python Package for MR Image Reconstruction. In ISMRM workshop on Data Sampling and Image Reconstruction, Jan 2020.
[2] Cherkaoui H, El Gueddari L, Lazarus C, Grigis A, Poupon F, Vignaud A, Farrens S, Starck JL, Ciuciu P. Analysis vs synthesis-based regularization for combined compressed sensing and parallel MRI reconstruction at 7 tesla. In 2018 IEEE 26th European Signal Processing Conference (EUSIPCO), Sep 2018 (pp. 36-40).
[3] El Gueddari L, Lazarus C, Carrié H, Vignaud A, Ciuciu P. Self-calibrating nonlinear reconstruction algorithms for variable density sampling and parallel reception MRI. In 2018 IEEE 10th Sensor Array and Multichannel Signal Processing workshop, Jul 2018 (pp.1-5).
[4] El Gueddari L, Chouzenoux E, Vignaud A, Ciuciu P. Calibration-less parallel imaging compressed sensing reconstruction based on OSCAR regularization. In 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Apr 2019.
[5] El Gueddari L, Chouzenoux E, Vignaud A, Pesquet JC, Ciuciu P. Online MR image reconstruction for compressed sensing acquisition in T2* imaging. In 2019 SPIE Conference – Wavelets and Sparsity XVIII, Aug 2019.