Context
In many scientific applications, increasingly large datasets are being acquired to describe more accurately biological or physical phenomena. While the dimensionality of the resulting measures has increased, the number of samples available is often limited, due to physical or financial limits. This results in impressive amounts of complex data observed in small batches of samples. A question that has arisen is then: what features in the data are really informative about some outcome of interest? This amounts to inferring the relationships between these variables and the outcome, conditionally to all other variables. Providing statistical guarantees on these associations is needed in many fields of data science, where competing models require rigorous statistical assessment. Yet reaching such guarantees is very hard. In particular, it is not uncommon for a brain imaging analysis task to have a sample size n of 100 but a covariates number p of 100000 that corresponds to the number of brain voxels. In such situation, a method to cluster the brain voxels into regions of voxels that works as a way of dimension reduction has been introduced.
Project FAST-BIG (ANR-17-CE23-0011 – Efficient statistical testing for high-dimensional models) aims at developing theoretical results and practical estimation procedures that render statistical inference feasible in such hard cases. We will develop the corresponding software and assess novel inference schemes on two applications: genomics and brain imaging.
Objectives
- The main objective of this project is to develop and extend theoretical results and practical estimation procedures that render statistical inference feasible in such high-dimensional setting.
- Potential development of robust methods to estimate the distribution of the covariates, especially the sample covariance matrix will also be considered.
- Development of the corresponding software and novelty assessment regarding the inference schemes with focus on application of brain imaging. Successful realizations of the procedures will be added to statistical, possibly domain-specific libraries, e.g. nilearn.github.io and ja-che.github.io/hidimstat/
Project members
- Principal Investigator: Bertrand Thirion (INRIA Parietal & Neurospin-CEA)
- Sylvain Arlot (Professor – Laboratoire de Mathématiques d’Orsay & INRIA Celest)
- Joseph Salmon (Professor – Universite de Montpellier)
- Binh Tuan Nguyen (PhD student – INRIA Parietal & Laboratoire de Mathématiques d’Orsay)
- Jérôme-Alexis Chevalier (PhD student – INRIA Parietal & Télécom ParisTech)
Software
Web Page
Main Results
A promising solution is to combine ensembling and clustering with a statistical inference algorithm:

Figure 1: Ensemble of Clustered Desparsified Lasso algorithm. The EnCluDL algorithm combines three algorithmic steps: a clustering (or parcellation) procedure applied to images, the Desparsified Lasso procedure (statistical inference) to derive statistical maps, and an ensembling method that synthesizes several statistical maps. In the first step, B clusterings of voxels are generated using B random subsamples of the original sample. Then, for each grouping-based data reduction, a statistical inference procedure is run resulting in B z-score maps (or p-value maps). Finally, these maps are ensembled into a final z-score map using an aggregation method that preserves statistical properties.
Spatial tolerance must be introduced to get statistical guarantees with clustered inference algorithms:
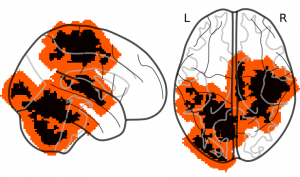
Figure 2: Spatial tolerance in the case of fMRI data: Expanding weight maps by 6 voxels (12 mm). The black-colored voxels represent the initial non zero weights of the reference map. The red-colored voxels are the δ-dilation of the previous map where δ = 6 voxels.

Figure 3: Spatial tolerance in the case of MEG data: Illustrating spatial tolerance of size δ = 20 mm and δ = 40 mm. The true source in red has a 10 mm radius (distance measured on the cortical surface) and the spatial tolerance extend this region by 20 mm on the left side and 40 mm on the right side in yellow.
Publications produced as the results of this project
- Chevalier, J. A., Salmon, J., & Thirion, B. (2018). Statistical inference with ensemble of clustered desparsified lasso. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 638-646). Springer, Cham.
- Nguyen T.-B., Chevalier J.-A., Thirion B., & Arlot S. (2020). Aggregation of Multiple Knockoffs. In Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, PMLR 128.
- Nguyen T.-B, J.-A Chevalier, & B. Thirion (2019). ECKO: Ensemble of Clustered Knockoffs for Robust Multivariate Inference on fMRI Data. In International Conference on Information Processing in Medical Imaging (pp. 454-466). Springer, Cham.

