Modeling and numerical simulation

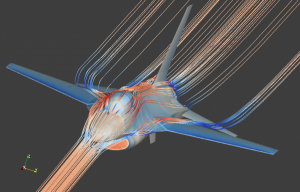
A major activity of Opale Project-Team concerns the development of numerical methods to solve partial differential equations, with a focus on finite-volume methods for hyperbolic systems (compressible flows, traffic models, etc). These developments are mainly implemented in NUM3SIS software platform, in the perspective of design optimization.

• Macroscopic traffic flow models

  Participants : P. Goatin, M. L. Delle Monache, M. Mimault, M. Twarogowska

  The modeling and analysis of traffic phenomena can be performed at a macroscopic scale by using partial differential equations derived from fluid dynamics. Such models give a description of collective dynamics in terms of the spatial density and average velocity. Continuum models have shown to be in good agreement with empirical data. Moreover, they are suitable for analytical investigations and very efficient from the numerical point of view. Therefore, they provide the right framework to state and solve control and optimization problems. Finally, they contain only few variables and parame- ters and they can be very versatile in order to describe different situations encountered in practice.

  The major mathematical difficulties related to this study follow from the mandatory use of weak (possibly discontinuous) solutions in distributional sense. Indeed, due to the presence of shock waves and interactions among them, standard techniques are gener- ally useless for solving optimal control problems, and the available results are scarce and restricted to particular and unrealistic cases. This strongly limits their applicability.

  Our scope is to develop a rigorous analytical framework and fast and efficient numerical tools for solving optimization and control problems, such as queues lengths control or buildings exits design. This will allow to elaborate reliable predictions and to optimize traffic fluxes. To achieve this goal, we will move from the detailed structure of the solutions in order to construct ad hoc methods to tackle the analytical and numerical difficulties arising in this study.

• Modeling cell dynamics

  Participants : A. Habbal

  A particular effort has been made to apply our expertise to solid and fluid mechanics, shape and topology design, multidisciplinary optimization by game strategies in biology and medicine. Two selected applications are privileged: solid tumors and wound healing. OPALE’s objective is to push further the investigation of these applications, from a mathematical-theoretical viewpoint and from a computational and software development viewpoint as well. These studies are led in collaboration with biologists, as well as image processing specialists.
  We have developed, and validated against biological experiments, two different math- ematical models which describe, at the macroscopic level, the dorsal closure of drosophila and the wound healing of MDCK cell-sheets. Our next objectives were the modeling of the interaction with vesicle trafficking, the establishment of mean field behavior and the study of the link between migration and actin dynamics. These objectives were partially fulfilled. We led a published study on the role of actin cable contraction in the drosophila dorsal closure and in wound healing as well. We also successfully led a study on the influ- ence of migration activators and inhibitors on the validity of F-KPP systems to describe the MDCK cell-sheet movement.

• Inverse problems solved as Nash games

  Participants : A. Habbal

  The majority if not all of the inverse boundary value problems IBVP are formulated as nonlinear minimization problems where the costs are made of antagonistic terms, some related to fidelity to the measured data against those who are dedicated to regularization needs. We investigate the ability of Nash game-theoretic formulations to properly handle such problems. This quite original idea was implemented to solve elliptic Cauchy problems (also known as data completion) and in mathematical image processing.

• Isogeometric analysis and design

  Participants : R. Duvigneau

  Design optimization stands at the crossroad of different scientific fields (and related software): Computer- Aided Design (CAD), Computational Fluid Dynamics (CFD) or Computational Structural Dynamics (CSM), parametric optimization. However, these different fields are usually not based on the same geometrical representations. CAD software relies on Splines or NURBS representations, CFD and CSM software uses grid-based geometric descriptions (structured or unstructured), optimization algorithms handle specific shape parameters. Therefore, in conventional approaches, several information transfers occur during the design phase, yielding approximations and non-linear transformations that can significantly deteriorate the overall efficiency of the design optimization procedure. The isogeometric approach proposes to definitely overcome this difficulty by using CAD standards as a unique representation for all disciplines. The isogeometric analysis consist in developing methods that use NURBS representations for all design tasks:

  • the geometry is defined by NURBS surfaces;
  • the computation domain is defined by NURBS volumes instead of meshes;
  • the solution fields are obtained by using a finite-element approach that uses NURBS basis functions instead of classical Lagrange polynomials;
  • the optimizer controls directly NURBS control points.

  Using such a unique data structure allows to compute the solution on the exact geometry (not a discretized geometry), obtain a more accurate solution (high-order approximation), reduce spurious numerical sources of noise that deteriorate convergence, avoid data transfers between the software. Moreover, NURBS representations are naturally hierarchical and allows to define multi-level algorithms for solvers as well as optimizers.

  

   

Optimization and control

• Algorithms for multidisciplinary optimization

  Participants : J.-A. Désidéri, A. Zerbinati

  Our approach to competitive optimization is based on a particular construction of Nash games, relying on a split of territory in the assignment of individual strategies. A methodology has been proposed for the treatment of two-discipline optimization problems in which one discipline, the primary discipline, is preponderant, or fragile. Then, it is rec- ommended to identify, in a first step, the optimum of this discipline alone using the whole set of design variables. Then, an orthogonal basis is constructed based on the evaluation at convergence of the Hessian matrix of the primary criterion and constraint gradients. This basis is used to split the working design space into two supplementary subspaces to be assigned, in a second step, to two virtual players in competition in an adapted Nash game, devised to reduce a secondary criterion while causing the least degradation to the first. The formulation has been proved to potentially provide a set of Nash equilibrium solutions originating from the original single-discipline optimum point by smooth contin- uation, thus introducing competition gradually. This approach has been demonstrated originally over a test-case of aero-structural aircraft wing shape optimization, in which the eigensplit-based optimization had revealed clearly superior.

  In a way somewhat complementary to the above competitive approaches, cooperative algorithms have been devised as methods of differentiable optimization to identify Pareto sets, in fairly general situations. Our approach is based on a simple lemma of convex analysis: in the convex hull of the gradients, there exists a unique vector of minimal norm, ω; if it is nonzero, the vector ω is a descent direction common to all criteria; otherwise, the current design point is Pareto-optimal. This result led us to generalize the classical steepest-descent algorithm by using the vector ω as search direction. We refer to the new algorithm as the multiple-gradient descent algorithm (MGDA). The MGDA yields to a point on the Pareto set, at which a competitive optimization phase can possibly be launched on the basis of the local eigenstructure of the different Hessian matrices.

• Uncertainty quantification and robust design

  Participants : D. Maruyama, R. Duvigneau

  A major issue in design optimization is the capability to take uncertainties into account during the design phase. Indeed, most phenomena are subject to uncertainties, arising from random variations of physical parameters, that can yield off-design performance losses. To overcome this difficulty, a methodology for robust design is currently developed and tested, that includes uncertainty effects in the design procedure, by maximizing the expectation of the performance while minimizing its variance.

  Two strategies to propagate the uncertainty are currently under study :

  • the use of metamodels for functional uncertainty estimation : a few simulations are performed for different values of the uncertain parameters in order to build metamodels, used to estimate some statistical quantities (expectation and variance) of the objective function and constraints, using a Monte-Carlo method.
  • the use of sensitivity analysis for field uncertainty estimation : we compute the derivatives of the flow output with respect to input parameters, such as shape or boundary conditions parameters. Then, flow variance can be estimated on the basis of these derivatives and input variance.

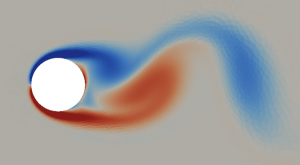
• Flow control

  Participants : J. Labroquère, R. Duvigneau

  To improve the aerodynamic performance of bluff-bodies, for which the flow is characterized by a massive detachment, control devices are introduced (pulsating jet, suction of blowing jet, etc) to modify the vortex generation process. In this context, optimization methods are used to determine suitable control parameters, such as frequency, amplitude or device location. This is a particularly tedious exercise from optimization point of view, because of the computational cost of the simulations (unsteady turbulent flows).

  Therefore, we are studying particular optimization strategies, based either on surrogate models or unsteady sensitivity informations, to derive efficient flow device parameters.

  

  

• Optimization in non-linear Mechanics

  Participants : A. Benki, A. Habbal, F.-Z. Oujebbour

  We study the ability of Simultaneous Perturbation Stochastic Approximation (SPSA) methods to replace the deterministic gradient information. The main applica- tion area is the multicriteria nonlinear structural optimization (elasto-plastic models). We have successfully coupled SPSA approximation to Simulated Annealing algorithms, and used the hybrid SA+SPSA approach to drive methods like as Normal Boundary Inter- section NBI, and Normalized Normal Constraint Method NNCM, which are dedicated to efficient capture of Pareto Fronts

Software environnements

• Resilience for e-Science applications

  Participants : T. Nguyên, L. Trifan

  Large-scale multidiscipline applications require high-performance computing (HPC) resources, which might be distributed over broadband networks. They can last for hours and even days.
  HPC infrastructures are known to be error-prone. The deployment costs of such applications require therefore effective fault-tolerance features. The project OPALE is exploring the design and implementation of resilience algorithms to restore and resume such applications after failures and unexpected behavior.
  Asymmetric checkpoints have been designed to reduce the size and restore overheads in case of failures. Experiments are made using the Grid5000 middleware for engineering applications deployed and monitored using the YAWL workflow management system. They involve distributed CFD, optimization and visualization software running on remote HPC clusters. They are invoked through Web services.

Nice-Matin article on Paola GOATIN’s research