Presentation
Core statistics and ML-development
Machine learning for inverse problems
From linear inverse problems to simulation based inference
Bi-level optimization
Reinforcement learning for active k-space sampling
Statistics and causal inference in high dimension
Conditional inference in high dimension
Post-selection inference on image data
Causal inference for population analysis
Machine Learning on spatio-temporal signals
Injecting structural priors with Physics-informed data augmentation
Learning structural priors with self-supervised learning
Revealing spatio-temporal structures in physiological signals
Application domains
MIND is driven by various applications in the data-driven neuroscience fields, which are largely part of the team members’ expertise.
Population modeling, large-scale predictive modeling
Unveiling Cognition Through Population Modelling
Imaging for health in the general population
Proxy measures of brain health
Studying brain age using electrophysiology
Proxy measures of mental health beyond brain aging
Mapping cognition & brain networks
Modeling clinical endpoints
EEG-based modeling of clinical endpoints
MRI-based modeling of clinical endpoints
From brain images and bio-signals to quantitative biology and physics
Statistics and causal inference in high dimension
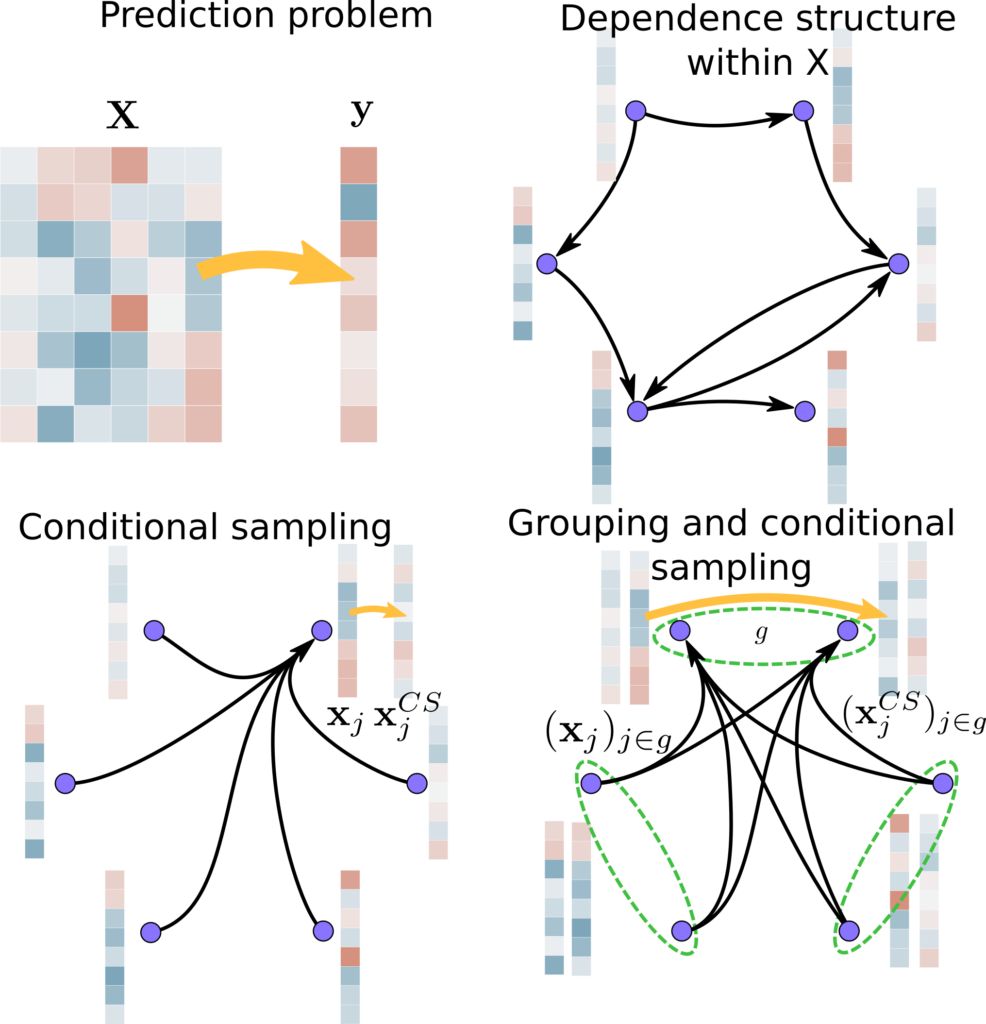
Statistics is the natural pathway from data to knowledge. Using statistics on brain imaging data involves dealing with high-dimensional data that can induce intensive computation and low statistical power. Besides, statistical models on large-scale data also need to take into account potential confounding effects and heterogeneity. To address these questions the MIND team employ causal modeling and post-selection inference. Conditional and post-hoc inference are rather short-term perspectives, while the potential of causal inference stands as a longer-term endeavour.
Heterogeneous Data & Knowledge Bases
Inferring the relationship between the physiological bases of the human brain and its cognitive functions requires articulating different datasets in terms of their semantics and representation. Examples of these are spatio-temporal brain images; tabular datasets; structured knowledge represented as ontologies; and probabilistic datasets. Developing formalisms that can integrate across all these modalities requires developing formalisms able to represent and efficiently perform computations on high-dimensional datasets as well as to combine hybrid data representations in deterministic and probabilistic settings. We will take on two main angles to achieve this task, the automated inference of cross-dataset features, or coordinated representations; and the use of probabilistic logic for knowledge representation and inference. The probabilistic knowledge representation part is now well advanced with the Neurolang project. It is yet a long-term endeavour. The learning of coordinated representations is less advanced.
Learning coordinated representations
Probabilistic Knowledge Representation
Activity
Results
New results
Accelerated acquisition in MRI
MRI is a widely used neuroimaging technique used to probe brain tissues, their structure and provide diagnostic insights on the functional organization as well as the layout of brain vessels. However, MRI relies on an inherently slow imaging process. Reducing acquisition time has been a major challenge in high-resolution MRI and has been successfully addressed by Compressed Sensing (CS) theory. However, most of the Fourier encoding schemes under-sample existing k-space trajectories which unfortunately will never adequately encode all the information necessary. Recently, the Mind team has addressed this crucial issue by proposing the Spreading Projection Algorithm for Rapid K-space sampLING (SPARKLING) for 2D/3D non-Cartesian T2* and susceptibility weighted imaging (SWI) at 3 and 7 Tesla (T) 123, 124, 107. These advancements have interesting applications in cognitive and clinical neuroscience as we already have adapted this approach to address high-resolution functional and metabolic (Sodium 23Na) MR imaging at 7T – a very challenging feat 1. However, the original SPARKLING trajectories are prone to off-resonance effects due to susceptibility artifacts. Therefore, we have extended the original SPARKLING methodology and developed the MORE-SPARKLING (Minimized Off-Resonance Effects) approach to correct for these artifacts. The fondamental idea implemented in MORE-SPARKLING is to make different k-space trajectories more homogeneous in time, in the sense that samples supported by different trajectories that are close in k-space must be collected at approximately the same time point. This allows us to mitigate the issue of off-resonance effects (signal void, geometric distortions) without increasing the scan time, as MORE-SPARKLING trajectories have exactly the same duration as their SPARKLING ancestor. This approach has been published 2 and is illustrated in Fig. 1. A patent application has been filed by the CEA for MORE-SPARKLING.
Complementary to that, we have also extended SPARKLING in another direction, namely the way we sample the center of k-space and proposed the GoLF-SPARKLING version in the same paper 2. The core idea here is to reduce the over-sampling of the center of k-space and grid it to collect Cartesian data and make notably the estimation of sensitivity maps in multicoil acquisition easier. Similarly to MORE-SPARKLING, a patent application has been filed for GoLF-SPARKLING.
Comparison between the original SPARKLING and the new MORE-SPARKLING 3D sampling patterns in k-space for accelerated MRI in presence of. The sampling patterns are shown on the left.
(A): Cartesian reference acquisition.
(B):
(C): Reconstructed 3D MR volume using the SPARKLING acquisition. Signal losses are depicted by blue arrows. (D): Reconstructed 3D MR volume using the MORE-SPARKLING version. The recovered signal is pointed with blue arrows. Minor artifacts are still there and depicted with orange/red arrows.
Additionally, we have shown that 3D-SPARKLING is a viable imaging technique and good alternative to Echo Planar Imaging for resting-state and task-based fMRI 4. This is illustrated in Fig. 2 during a retinotopic mapping experiment which consists in mapping the retina to the primary visual cortex. These results have been obtained at a 1mm isotropic resolution both for EPI and SPARKLING acquisitions.
Projection of the BOLD phase maps on the pial surface visualized on the inflated surface for participants V#3 (3D-SPARKLING run first) and V#4 (3D-EPI run first). 3D-SPARKLING yields improved projected BOLD phase maps for V#3 in comparison with 3D-EPI both on raw and spatially smoothed data. Opposite results were found in favor of 3D-EPI in V#4, notably on spatially smoothed data.
Deep learning for MR image reconstruction and artifact correction
Although CS is used extensively, this approach suffers from a very slow image reconstruction process, which is detrimental to both patients and rapid diagnosis. To counteract this delay and improve image quality, as explained in Sec. 3.1 deep learning is used. In 2020 we secured the second spot in the 2020 brain fastMRI challenge (1.5 and 3T data) 139 with the XPDNet (Primal Dual Network where X plays the role of a magic card) deep learning architecture. Additionally, we assessed XPDNet’s transfer learning capacity on 7T NeuroSpin T2 images. However this DL reconstruction process was limited to Cartesian encoding, thus incompatible with our SPARKLING related technological push. In 2022, we went therefore further by proposing the NCPD-Net deep learning architecture for non-Cartesian imaging. NCPD-Net stands for Non-Cartesian Primal Dual Network and is able to handle both 2D and 3D non-Cartesian k-space data such as those collected with the full 3D SPARKLING encoding scheme 154. This progress allowed us to make a significant leap in image quality when implementing high resolution imaging while maintaining a high acceleration rate.
In 2023, we published novel significant results based on the original NC-PDNet archiecture. We actually combined with physics-driven model to speed up the correction of off-resonance effects induced by the inhomogeneities of the static magnetic field
Deep learning physics-informed correction of off-resonance artifacts during MR image reconstruction using the NC-PDnet architecture. Illustration on a single SWI volume (high resolution: 600
Left(red): Compressed Sensing (CS) reconstruction with no artifact correction, computed in 25min.
Center left: CS reconstruction using a reduced non-Fourier forward model to correct for
Middle(purple): Network or NC-PDnet based reconstruction without physics based knowledge to correct for
Center right(blue): NC-PDnet based reconstruction without physics based knowledge to correct for
Right(green): Classical CS reconstruction and off-resonance artifact correction based on an extended non-Fourier model, which costs 8 hours of computation. The best result is that in the blue frame.
MRI magnetic resonance imaging essentially involves the optimization of (1) the sampling pattern in k-space under MR hardware constraints and (2) image reconstruction from undersampled k-space data. Recently, deep learning methods have allowed the community to address both problems simultaneously, especially in the non-Cartesian acquisition setting. In 2023, the MIND has made major contribution 9 to this field by tackling some major concerns in existing approaches. Particularly, current state-of-the-art learning methods seek hardware compliant k-space sampling trajectories by enforcing the hardware constraints through additional penalty terms in the training loss. Through ablation studies, we rather show the benefit of using a projection step to enforce these constraints and demonstrate that the resulting k-space trajectories are more flexible under a projection-based scheme, which results in superior performance in reconstructed image quality. In 2D studies, our novel PROjection for Jointly lEarning non-Cartesian Trajectories while Optimizing Reconstructor (PROJeCTOR) trajectories present an improved image reconstruction quality at a 20-fold acceleration factor on the fastMRI data set with SSIM scores of nearly 0.92–0.95 in our retrospective studies as compared to the corresponding Cartesian reference and also see a 3–4 dB gain in PSNR as compared to earlier state-of-the-art methods. Finally, we extend the algorithm to 3D and by comparing optimization as learning-based projection schemes in Fig. 4, we show that data-driven joint learning-based PROJeCTOR trajectories outperform model-based methods such as SPARKLING through a 2 dB gain in PSNR and 0.02 gain in SSIM.
A generic learning-based framework for joint optimization of the MRI acquisition and reconstruction models. Qualitative and quantitative comparisons of reconstructed images from 3D
(B)SPARKLING and
(C)PROJeCTOR trajectories at an acceleration factor AF = 20 as compared to
(A)Cartesian reference. The reconstructed images are shown in the top row, while the residuals are shown in the bottom. Further, box plots of the SSIM and PSNR scores on 20 test data sets are shown in the bottom-left. The significance levels are marked through a paired samples Wilcoxon test.
Large Scale Bayesian Network Resolution with Applications to Neuroimaging
Bayesian networks (BNs) have emerged as a powerful tool for modeling complex relationships among variables in neuroimaging data generatively. Their ability to capture causal and probabilistic dependencies makes them well-suited for representing the intricate and multifaceted nature of brain activity. However, the large scale of neuroimaging data presents a significant challenge for BNs. This data in a large database can scale to millions of random variables, if we consider 1,000 subjects with at least 32,000 measurements on the brain cortex per subject. As the number of variables increases, the complexity of the BN grows exponentially, making it computationally intractable to fit these models using existing generic algorithms. This computational bottleneck impedes the widespread application of BNs in neuroimaging research and hinders our ability to fully understand the intricate workings of the brain.
To address this problem we have porposed the PAVI method (Plate Amortized Variational Inference) 158 as a follow up of our previously proposed Automatic Dual Amortized Variational Inference (ADAVI) 159. These methods harness the symmetry of large neuroimaging models, specifically considering each cortical measurement and each subject as independent identically distributed realizations of the same random variables. In complement with stochastic optimization techniques, the PAVI algorithm is able to produce individualized parcellations of 1,000 of subjects at a time. Thus, we are now able to harness the descriptive and interpretable power of BNs to produce individualized cortical parcellations which we then test through the prediction of cognitive abilities.
Generalized parametric models for temporal point processes
Temporal point processes (TPP) are a natural tool for modeling event-based data. Among all TPP models, Hawkes processes have proven to be the most widely used, mainly due to their adequate modeling for various applications, particularly when considering exponential or non-parametric kernels. Although non-parametric kernels are an option, such models require large datasets. While exponential kernels are more data efficient and relevant for specific applications where events immediately trigger more events, they are illsuited for applications where latencies need to be estimated, such as in neuroscience. We developed an efficient solution to TPP inference using general parametric kernels with finite support. The developed solution consists of a fast
sampleMEG dataset, and their respective estimated intensity functions after a stimulus (cue at time = 0 s), for auditory and visual stimuli with non-parametric (NP), Truncated Gaussian (TG) and Raised Cosine (RC) kernels. The parametric kernels recover cleaner estimates of the brain response to the stimuli compare to NP, and both estimate correctly the link between the stimuli and the response.
Statistically Valid Variable Importance Assessment through Conditional Permutations
Variable importance assessment has become a crucial step in machine-learning applications when using complex learners, such as deep neural networks, on large-scale data. Removal-based importance assessment is currently the reference approach, particularly when statistical guarantees are sought to justify variable inclusion. It is often implemented with variable permutation schemes. On the flip side, these approaches risk misidentifying unimportant variables as important in the presence of correlations among covariates. Here we develop a systematic approach for studying Conditional Permutation Importance (CPI) that is model agnostic and computationally lean, as well as reusable benchmarks of state-of-the-art variable importance estimators. We show theoretically and empirically that CPI overcomes the limitations of standard permutation importance by providing accurate type-I error control. When used with a deep neural network, CPI consistently showed top accuracy across benchmarks. An experiment on real-world data analysis in a largescale medical dataset showed that CPI provides a more parsimonious selection of statistically significant variables. Our results suggest that CPI can be readily used as drop-in replacement for permutation-based methods.
Performance of Conditional permutation-based vs standard permutation-based variable importance: Performance at detecting important variables on simulated data with
(A): The type-I error quantifies to which extent the rate of low p-values (
(B): The AUC score measures to which extent variables are ranked consistently with the ground truth. Dashed line: targeted type-I error rate. Solid line: chance level.
False Discovery Proportion control for aggregated Knockoffs
Controlled variable selection is an important analytical step in various scientific fields, such as brain imaging or genomics. In these high-dimensional data settings, considering too many variables leads to poor models and high costs, hence the need for statistical guarantees on false positives. Knockoffs are a popular statistical tool for conditional variable selection in high dimension. However, they control for the expected proportion of false discoveries (FDR) and not their actual proportion (FDP). We present a new method, KOPI, that controls the proportion of false discoveries for Knockoff-based inference. The proposed method also relies on a new type of aggregation to address the undesirable randomness associated with classical Knockoff inference. We demonstrate FDP control and substantial power gains over existing Knockoff-based methods in various simulation settings and achieve good sensitivity/specificity tradeoffs on brain imaging and genomic data.
Application of Kopi to cognitive brain imaging.We have employed KOPI on fMRI and genomics data. The aim of fMRI data analysis is to recover relevant brain regions for a given cognitive task as shown below. Here we display brain regions whose activity predicts that the participant is atending to stimuli with social motion.
Activity reports
Overall objectives
The Mind team, which finds its origin in the Parietal team, is uniquely equipped to impact the fields of statistical machine learning and artificial intelligence (AI) in service to the understanding of brain structure and function, in both healthy and pathological conditions.
AI with recent progress in statistical machine learning (ML) is currently aiming to revolutionize how experimental science is conducted by using data as the driver of new theoretical insights and scientific hypotheses. Supervised learning and predictive models are then used to assess predictability. We thus face challenging questions like Can cognitive operations be predicted from neural signals? or Can the use of anesthesia be a causal predictor of later cognitive decline or impairment?
To study brain structure and function, cognitive and clinical neuroscientists have access to various neuroimaging techniques. The Mind team specifically relies on non-invasive modalities, notably on one hand, magnetic resonance imaging (MRI) at ultra-high magnetic field to reach high spatial resolution and, on the other hand, electroencephalography (EEG) and magnetoencephalography (MEG), which allow the recording of electric and magnetic activity of neural populations, to follow brain activity in real time. Extracting new neuroscientific knowledge from such neuroimaging data however raises a number of methodological challenges, in particular in inverse problems, statistics and computer science. The Mindproject aims to develop the theory and software technology to study the brain from both cognitive to clinical endpoints using cutting-edge MRI (functional MRI, diffusion weighted MRI) and MEG/EEG data. To uncover the most valuable information from such data, we need to solve a large panoply of inverse problems using a hybrid approach in which machine or deep learning is used in combination with physics-informed constraints.
Once functional imaging data is collected the challenge of statistical analysis becomes apparent. Beyond the standard questions (Where, when and how can statistically significant neural activity be identified?), Mind is particularly interested in addressing driving effect or the cause of such activity in a given cortical region. Answering these basic questions with computer programs requires the development of methodologies built on the latest research on causality, knowledge bases and high-dimensional statistics.
The field of neuroscience is now embracing more open science standards and community efforts to address the referenced to as “replication crisis” as well as the growing complexity of the data analysis pipelines in neuroimaging. The Mindteam is ideally positioned to address these issues from both angles by providing reliable statistical inference schemes as well as open source software that are compliant with international standards.
The impact of Mindwill be driven by the data analysis challenges in neuroscience but also by the fundamental discoveries in neuroscience that presently inspire the development of novel AI algorithms. The Parietal team has proved in the past that this scientific positioning leads to impactful research. Hence, the newly created Mind team formed by computer scientists and statisticians with a deep understanding of the field of neuroscience, from data acquisition to clinical needs, offers a unique opportunity to expand and explore more fully uncharted territories.



