Context
We consider the numerical simulation of flows involving complex geometries, as well as the evolution of complex nonlinear fronts. Applications can be found in several domains wing icing, atmospheric re-entry, natural hazards, etc.
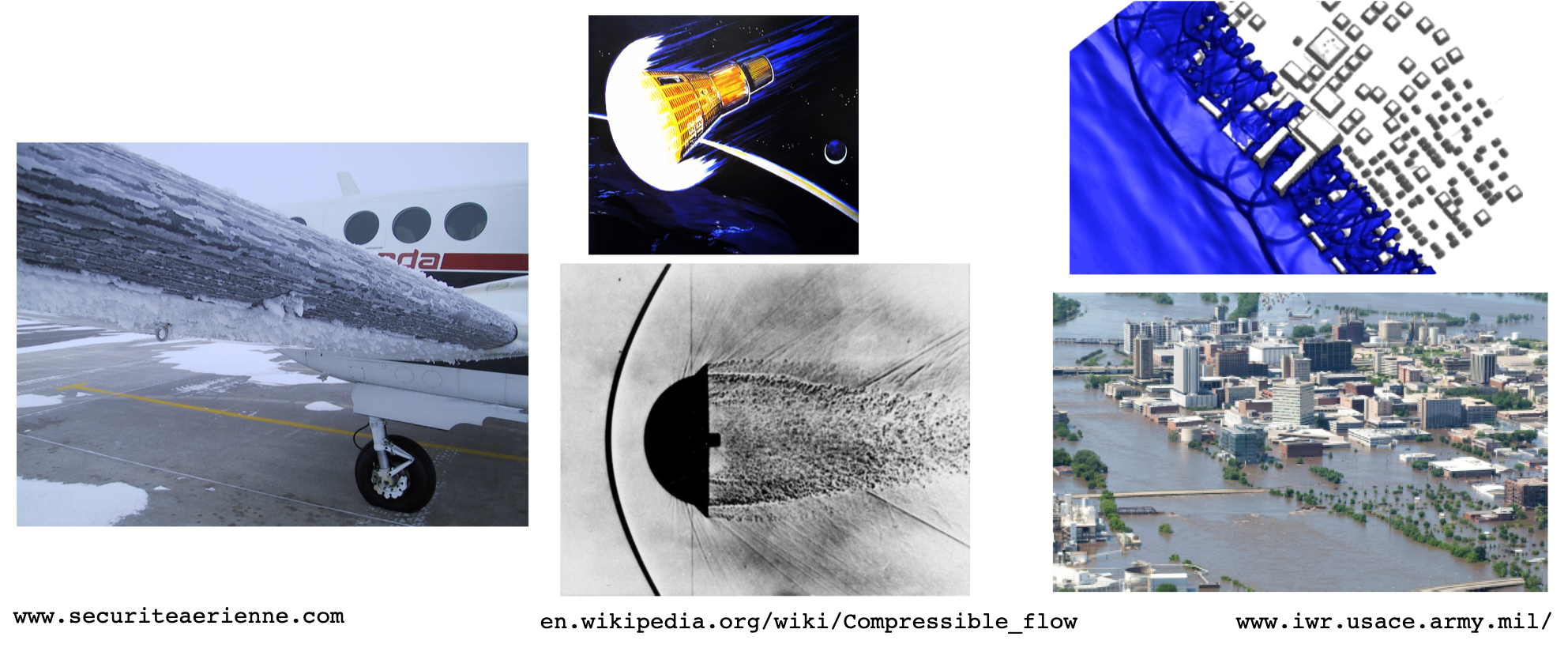
Our aim is to be able to construct numerical methods allowing a flexible approximation in terms of both the underlying discretization technique (finite volume, finite elements, residual distribution, and finite differences), and of the meshing strategy (Cartesian, unstructured, adapted or not).
We thus consider the construction of error controlled approaches to solve complex PDEs on unfitted meshes. The challenge is to represent (possibly nonlinear) relations formulated on a certain boundary or front, on a discrete/surrogate boundary composed of mesh faces. Error control is achieved either by of appropriate sub-grid models allowing to correct for both geometrical and physical approximations. These sub-grid approximations may or may not be combined with mesh adaptation to further enhance the discrete resolution.
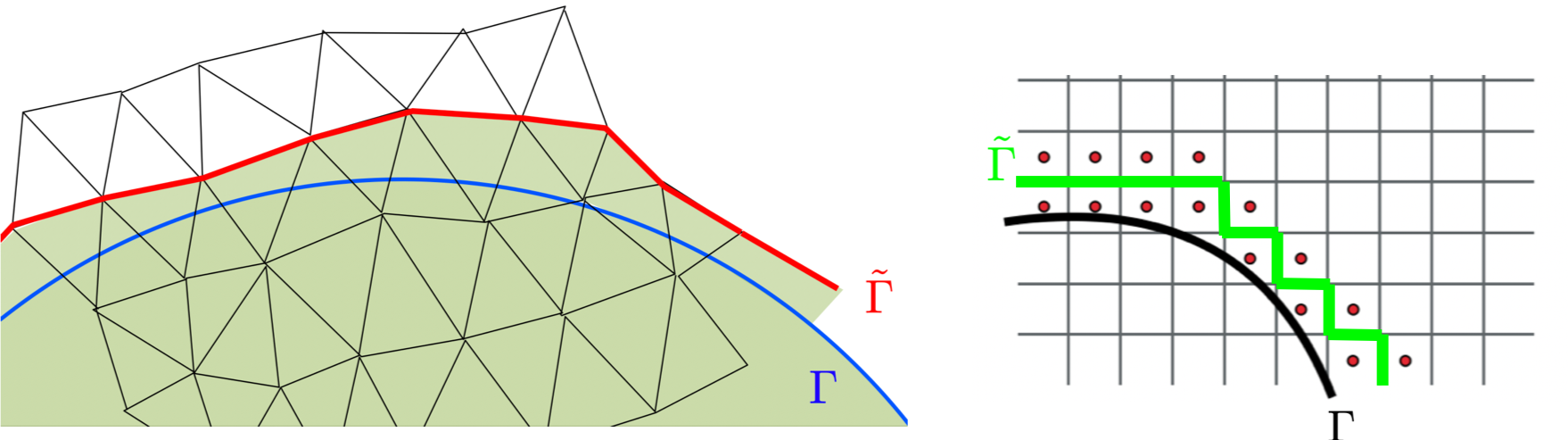
Methods and examples
Immersed boundaries
Embedded approaches with high order correction (SBM)
References
T.Carlier, L. Nouveau, H. Beugendre, M. Colin and M. Ricchiuto. An Enriched Shifted Boundary Method to Account For Moving Fronts, submitted to J.Comput.Phys, preprint
L. Arpaia, H. Beaugendre, L. Cirrottola, A. Froehly, M. Lorini, L. Nouveau and M. Ricchiuto. h- and r- adaptation on simplicial meshes using mmg tools. In Mesh Generation and Adaptation. Cutting-Edge Techniques, SEMA-SIMAI. Springer, 2022 preprint
M. Ciallella, M. Ricchiuto, R. Paciorri, and A. Bonfiglioli. Extrapolated DIscontinuity Tracking for complex 2D shock interactions, Computer Methods in Applied Mechanics and Engineering 391, 2022 preprint
B. Constant, S. Péron, H. Beaugendre and C. Benoit, An improved Immersed Boundary Method for turbulent flow simulations on Cartesian grids Journal of Computational Physics, Vol 435, 2021, preprint
M. Ciallella, M. Ricchiuto, R. Paciorri, and A. Bonfiglioli. Extrapolated Shock-Tracking: bridging fitting and embedded boundary methods to handle shock waves, J. Comput. Phys. 412, 2020 preprint
L. Nouveau, M. Ricchiuto, and G. Scovazzi. High-Order Gradients with the Shifted Boundary Method: An Embedded Enriched Mixed Formulation for Elliptic PDEs, J. Comput. Phys. 398, 2019 preprint
T. Song, A. Main, G. Scovazzi, and M. Ricchiuto. The shifted boundary method for hyperbolic systems: embedded computations of linear waves and shallow water flows, J.Comput.Phys. 369, pp. 45-79, 2018 preprint
L. Nouveau, H. Beaugendre, C. Dobrzynski, R. Abgrall and M. Ricchiuto. An adaptative, residual based, splitting approach for the penalized Navier Stokes equations, Computer Methods in Applied Mechanics and Engineering 303, pp 208–230, 2016 preprint
