A tidal bore is is a sudden elevation of the water surface that travels upstream an estuary with the incoming flood tide. A tidal bore can be schematically represented by a propagating transition between two streams of water depth. Denoting by 1 the state ahead of the bore and by 2 the state behind it the two streams are characterized by different water depths h1 and h2, with h1<h2.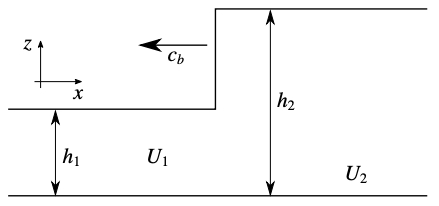 
The intensity of two-dimensional bores is mainly characterized by the Froude number. When the Froude number (Fr) is less than approximate 1.3, the bores are called undular bores and the bore transition is smooth and followed by wave trains, see here for more details. This phenomenon is a weakly dispersive non-hydrostatic process which can be modeled by Boussinesq-type equations. The bore dynamic in estuaries are controlled by three dimensionless parameters as shown by the experiments of Treske(1994) and by Bonneton et al (2015). These are the Froude number and the geometrical parameters W/h1 and tan β, where W and β are the characteristic bottom channel width and bed slope angle from horizontal respectively. Treske (1994) identified showed that
the secondary wave field is two-dimensional with strong variations in crest height across t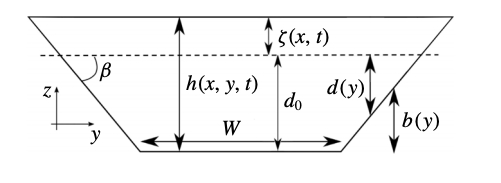
he channel section, and then strongly differs from that in rectangular channels. Treske (1994) identified a transition around Frt = 1.15. For Fr < Frt , the secondary wave wavelength in the whole channel is at least two to three times larger than in a rectangular channel for the same Froude numbers. For F > Frt however the secondary wave field along the channel axis becomes very similar to Favre waves (rectangular channels), while long wavelengths are still observed along the banks, leading to a
complex multi-dimensional wave structure.
We model this dynamic with a weakly dispersive Serre-Green-Naghdi approach reproducing numerically the experiments by Treske using the code SLOWS. Simulations have been performed for a range of Froude numbers from 1.02 to 1.275. 
The animations below show the evolution of the bore for Fr =1.05 and 1.2 respectively.
Both Treske(1994) and Bonneton et al. (2015) identified two undular bore regimes around a transition Froude number Frt of approximately 1.1: the high Froude number regime (HFN regime) for F > Frt and the low Froude number regime (LFN regime) for F < Frt. In the HFN regime, the secondary wave field is strongly
multi-dimensional and characterized by a ‘fish-tail’ pattern. The wave amplitude is maximum in the mid-channel and decreases toward the banks. It was shown that the amplitude and wavelength along the river axis
are similar to those of Favre waves in rectangular channels for the same Froude number. This observation indicates that this HFN regime is most probably controlled by dispersive non-hydrostatic processes as for the Favre waves. The secondary wave field in the LFN regime shows a significantly different behaviour. The phase structure is quasi-one-dimensional, and the wave amplitude is at its maximum on the banks and minimum in the mid-channel The transition between HFN and LFN regimes is marked by an abrupt decrease of the secondary wave steepness (Bonneton et al. 2015), and by a considerable increase in wavelength. The two undular bore regimes are simulated using SLOWS and the results are compared with the Treske’s experiment.
We used a range of Fr sufficiently large to study the LFN–HFN transition, while remaining well below the second transition to a fully breaking bore along the channel axis. We post processed the time series of the water elevation for all the simulated values of Fr to obtain the amplitude and trough of the first peak and the wavelength both for the channel axis (a) and the banks (b). 
Numerical results on the axis are denoted by circles and experimental data by x. For the sloping banks numerical results are denoted by squares and experimental data by +.
On the axis both experiments and simulations show a quasi-linear increase in the water elevation with the Froude number with no clear transition. On the banks we observe the transition taking place at Fr=1.15. The transition is also very clear in the wavelength distribution (c). We can see that the HFN regime is characterized by wavelengths on the axis very close to these observed in straight channels. 
References
R. Chassagne, A.G. Filippini, M. Ricchiuto and P. Bonneton, Dispersive and dispersive-like bores in channels with sloping banks, Journal of Fluid Mechanics 870, pp. 595-616, 2019 pdf
A.G. Filippini, L. Arpaia, P. Bonneton, and M. Ricchiuto, Modelling analysis of tidal bore formation in convergent estuaries, Eur.J.Mech. – B/Fluids 73, 2019 pdf
P. Bonneton, A. Filippini, L. Arpaia, N. Bonneton and M. Ricchiuto. Conditions for tidal bore formation in convergent alluvial estuaries. Estuarine, Coastal and Shelf Science, 172:121 – 127, 2016 preprint
P. Bonneton, N. Bonneton, J.P. Parisot, and B. Castelle. Tidal bore dynamics in funnel-shaped estuaries. J. Geophys. Res.: Ocean, 120(2), 2015 https://doi.org/10.1002/2014JC010267
A. Treske. Undular bores (favre-waves) in open channels – Experimental studies. J. of Hydraulic Research 32, 1994 https://doi.org/10.1080/00221689409498738
