This is one of the Benchamark Problems proposed by NTHMP Mapping and modelling Benchmarking Workshop: Tsunami Currents. Its is widely used to validate numerical codes for tsunami simulation. This experiment has a single solitary wave which propagating up a triangular shelf with a conical island located at the offshore point of the shelf. The data available involve a detailed topography, the positions as well the time histories of the free surface elevation of the water and the velocity in the wave gauges. 
We run the simulation solving a weakly dispersive fully nonlinear model using a splitting method implemented in the code SLOWS . For more information on the numerical scheme see [1, 2]. In order to reduce the computational time but being able to accurately resolve all the important phenomena taking place on the shelf and around the conical island we refine the mesh using the MMG library.
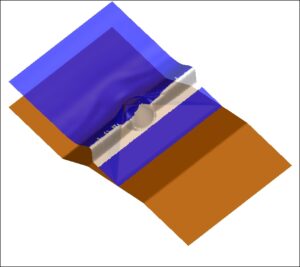
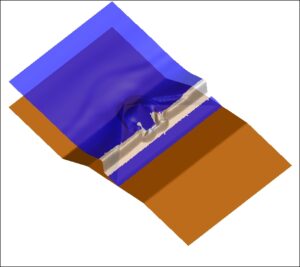
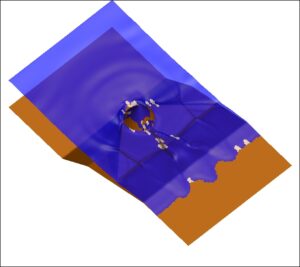
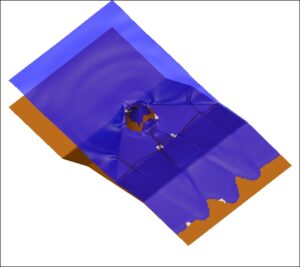
Next figures sow the computed free surface elevation at different time instants. With white collar we denote the time evolution of the breaking regions detected by the criteria of the breaking mechanism. As the solitary wave propagates toward the beach it shoals, increases its steepness and nonlinearity up to reaching a breaking point , when it reaches the apex of the triangle shelf. At time t=6.5sec the wave completely overtops the concrete cone, while on the two sides the surge continues to shoal, diffracting around the base of the cone. By t=8.5sec the refracted and diffracted waves, collide on the lee side of the self. After t = 9s, the water starts to withdraw from the con top and a bore-front forms, from the combined waves after the di raction, and propagates on the shelf behind the cone and then onshore. After t = 15s, a new bore is creates from the the drawn-down of the water and collides with the refracted waves.
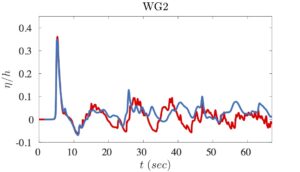
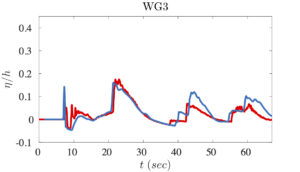
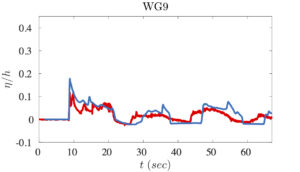
The availability of the data allows a quite extensive validation/verification of the hybrid numerical scheme implemented in SLOWS. This validation is reported below in terms of comparisons between simulations (blue lines) and experimental data (red lines) for some of the wave-gauges highlighted by black circles in the model picture above.
References
- M. Kazolea, A.G. Filippini, and M. Ricchiuto, A low dispersion finite volume/element method for nonlinear wave propagation, breaking and runup on unstructured meshes, submitted to Ocean Modelling, https://hal.inria.fr/hal-03402701
- A. Filippini, M. Kazolea and M. Ricchiuto. A flexible genuinely nonlinear approach for wave propagation, breaking and runup. J.Comput.Phys.,310:381–417, 2016. (PDF)