This part of our research focuses on the development of parallel algorithms for major kernels in numerical linear and multilinear algebra, that are building blocks of many applications in computational science (in particular the solvers developed in other research sections). The goal is to enable their efficient execution and scaling to emerging high-performance clusters with an increasing number of nodes. These algorithms feature two main characteristics:
- reducing or minimizing communication: we address one of the main challenges we face in high performance computing, the increased communication cost with respect to the computational cost.
- randomization: a powerful technique for solving large scale problems, that relies on dimension reduction through random projections.
We consider orthogonalization techniques and Krylov subspace methods and techniques for exploiting “data sparsity” (problems in which data can be compressed without significant loss of information). For these methods, we design novel algorithms and study their numerical stability and their performance on parallel computers.
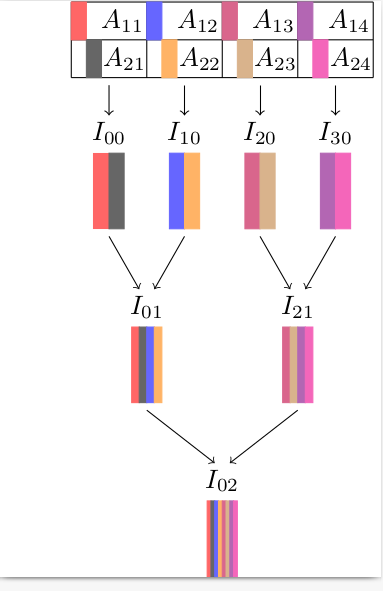
In the context of orthogonalization techniques, one of our main results is a randomized process for orhtogonalizing a set of vectors. Our randomized Gram-Schmidt orthogonalization process is as stable as MGS (modified Gram-Schmidt) and more efficient than CGS (classical Gram-Schmidt). The proposed Gram-Schmidt process can be applied to Arnoldi iteration and results in new Krylov subspace methods as randomized GMRES.
To exploit “data sparsity” as arising in computational chemistry or boundary element methods, we focus on low rank matrix and tensor approximations as well as fast matrix-vector products. For low rank matrix approximation, we developed both randomized and deterministic approaches. One of our main contributions is the introduction of a factorization that allows to unify and generalize many past algorithms, sometimes providing strictly better approximations. In the context of deterministic algorithms, we introduced novel algorithms for both dense and sparse matrices that minimize the number of messages exchanged between processors and have guarantees for the approximations of the singular values provided by the low rank approximation. In the specific context of Boundary Element Methods (BEM) we propose a linear-time approximation algorithm for admissible matrices obtained from the hierarchical form of Boundary Element matrices.
A recent research direction focuses on solving problems of large size that can feature high dimensions as in molecular simulations. The data in this case is represented by objects called tensors, or multilinear arrays. The goal is to design novel tensor techniques to allow their effective compression, i.e. their representation by simpler objects in small dimensions, while controlling the loss of information. For low rank tensor approximation, we have introduced new parallel algorithms that reduce communication by considering tensor representations as tensor train or Tucker format .
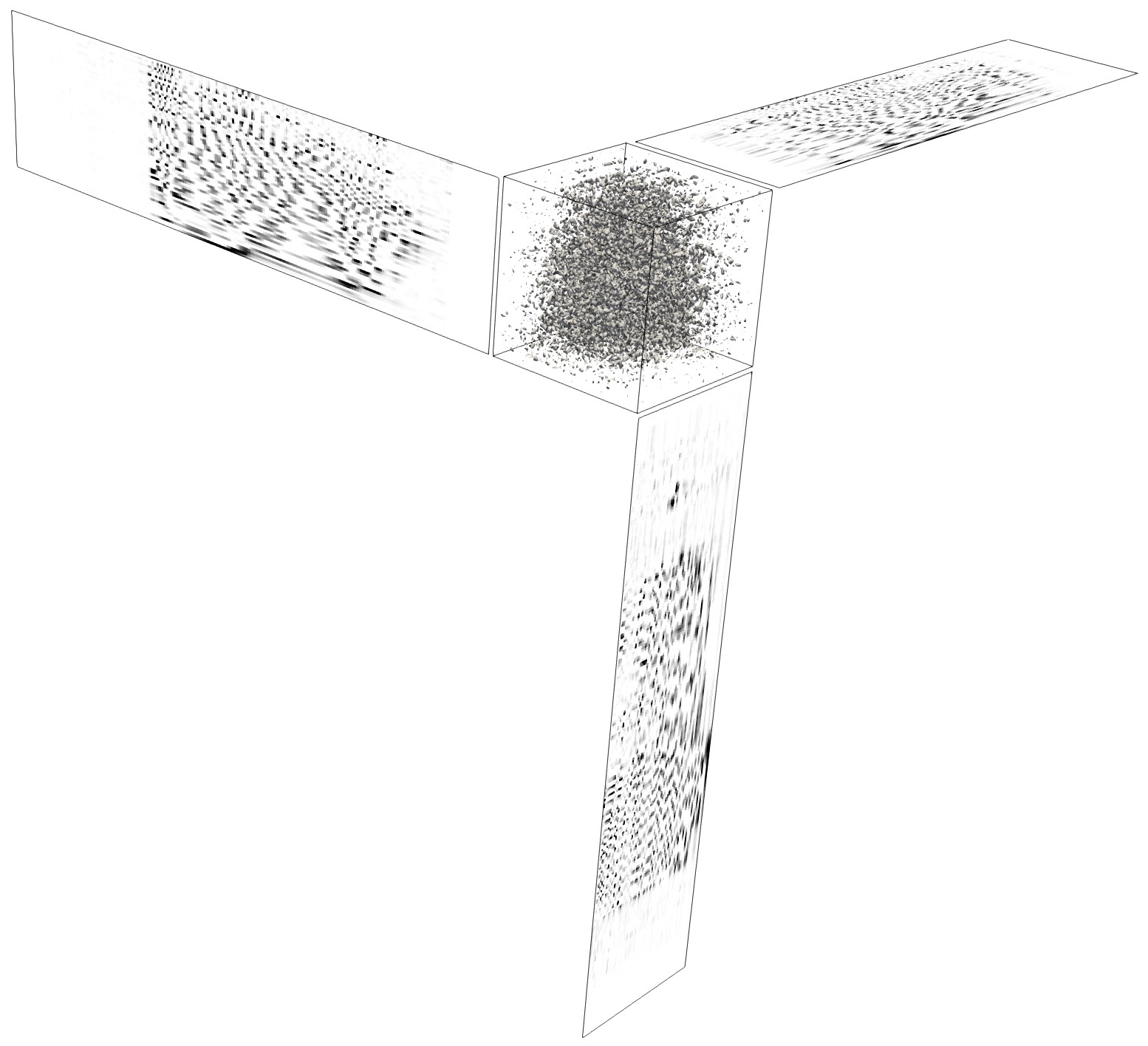
256×256×256 aneurysm tensor and its rank 64×64×64 Tucker decomposition computed with a Higher-Order QR with Tournament Pivoting algorithm. Please click to enlarge.
For fast matrix-vector products we use Fast Multipole Method and hierarchical matrices. This study led to the development of the HTool library which is interfaced with BemTool (to benefit from sophisticated assembly routines related to boundary element methods), FreeFEM and HPDDM.
Fast Multipole Methods (FMMs) based on the oscillatory Helmholtz kernel can reduce the cost of solving N-body problems arising from Boundary Integral Equations (BIEs) in acoustic or electromagnetism. However, their cost strongly increases in the high-frequency regime. We introduced a new directional FMM for oscillatory kernels (defmm – directional equispaced interpolation-based fmm), whose precomputation and application are FFT-accelerated due to polynomial interpolations on equispaced grids.
In the context of iterative methods, we continue our work on enlarged Krylov subspace solvers which allow to reduce the number of global communications while also increasing the arithmetic intensity of these methods. We study in particular enlarged GMRES and Conjugate Gradient, their convergence and their combination with deflation techniques, as well as more generally deflation techniques and block Krylov methods. Most of the developed algorithms are available in PreAlps library, while block methods and deflation are available in HPDDM .