Our research lines are motivated by our application fields, which we describe below (this list should not be considered as exhaustive):
Vehicular and pedestrian traffic flows
Traffic flow models are a commonly cited example of “complex systems”, in which individual behavior and self-organization phenomena must be taken into account to obtain a realistic description of the observed macroscopic dynamics. Intelligent Transportation Systems (ITS) is nowadays a booming sector, and the contribution of mathematical modeling and optimization is widely recognized. Further improvements require more advanced models, keeping better into account interactions at the microscopic scale.
Aerodynamic analysis and design
Shape optimization in compressible aerodynamics is still a challenging problem, due to the computational costs of high-fidelity simulations, the presence of local optima, the necessity of a tight integration with computational geometry, the possible crash of the evaluation procedure during mesh update or analysis, etc. We contribute to this topic by developing a fully integrated geometry-simulation-optimization framework based on a CAD-consistent Discontinuous Galerkin method within a Bayesian Optimization algorithm.

Flow simulation around an airfoil at high angle of attack (M=0.5, Re=5000), using a NURBS grid (degree 4, 13 millions of degrees of freedom, 480 cores)
Optimization of unsteady systems as multi-point problems
The optimization of unsteady systems is usually performed by minimizing a time-averaged criterion, which does not allow a very fine control of the phenomena. Alternatively, we consider the optimization of the unsteady system as a multi-point problem involving a large set of descent directions computed at each time step. (more)
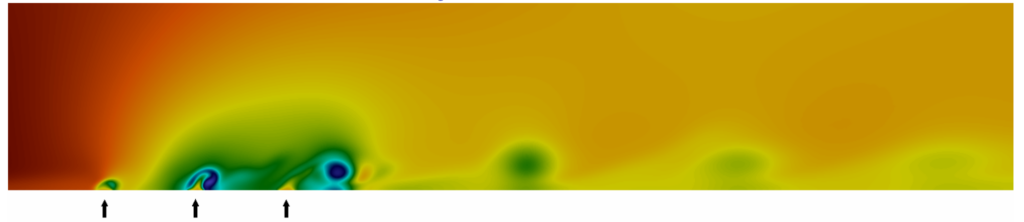
Flow over a flat plate equipped with three pulsating jets whose parameters are optimized (instantaneous density)
Prioritized multi-objective optimization of the flight performance of a SuperSonic Business Jet (SSBJ)
Fifteen sizing parameters defining a generic geometry of a Super Sonic Business Jet (SSBJ), all subject to interval bounds, have been optimized concurrently to maximize flight performance in terms of mass at take-off (to be minimized), range (to be maximized), approach speed (to be reduced) under a bound constraint on take-off distance. This optimization was conducted within the ANR Project “OMD” on multi-disciplinary optimization. The generic geometry was also utilized in the European Project HISAC. (more)
Prioritized multi-objective optimization of the structural strength
of a sandwich panel under bending loads and blast
In this example, a sandwich panel is optimally sized with respect to four criteria related to strength or blast mitigation. (more)
Civil building structures
We consider here topology and shape multi-objective optimization of civil building structures made of new materials, taking into consideration structural safety, energy cost, life cycle analysis and environmental impact. We notably aim to develop efficient methods to capture the Pareto front when the structures undergo uncertain loadings (magnitude, location, direction) or material properties.
Modeling cell dynamics
We intend to model, calibrate, validate and control the migration of multicellular structures. A first ongoing step is to connect activator-inhibitor (pharmaco) dynamics to the Fisher-KPP equation, then assess the ability of the obtained system to model exogeneously activated or inhibited MDCK (Madin-Darby Canine Kidney) cell sheet closure.