Return to Assoc. Team

NOLOCO

Efficient numerical schemes for non-local transport phenomena

Participants

At Inria:

Paola GOATIN  (PI) is Senior Researcher at Inria Centre of Université Côte d’Azur, leader of the ACUMES Project-Team. Expertise: analysis and numerical approximation of hyperbolic systems of conservation laws, application to traffic flow modeling.

Regis DUVIGNEAU is Senior Researcher at Inria Centre of Université Côte d’Azur, member of the ACUMES Project-Team. Expertise: numerical methods for simulation and optimization of complex flows.

Daniel INZUNZA is Postdoc at Inria Centre of Université Côte d’Azur, member of the ACUMES Project-Team. Expertise: High order finite volume schemes for nonlocal systems of conservation laws in two space dimension.

At University of Bio-Bio:

Luis Miguel VILLADA OSORIO (co-PI) is Professor and Program Director of Master in Mathematics at University of Bio-Bio, Chile, and External Associate Research at CI2MA University of Concepcion. Expertise: numerical methods for convection-diffusion systems, applications to traffic flows and polydisperse sedimentation.

Harold Deivi CONTRERAS is PhD student at University of Bio-Bio since 2020. Subject: Numerical analysis of balance/conservation laws with nonlocal and memory terms.

At Universidad de Concepcion:

Raimund BURGER is Full Professor and Sub-Director at Center for Research in Mathematical Engineering (CI2MA) at Universidad de Concepcion . Expertise: mathematical and numerical analysis, scientific computing and applications of systems of conservation laws and related equations, as well as of coupled flow-transport systems, with applications in mineral processing, wastewater treatment, bioprocesses and trac modeling.

Yessennia MARTINEZ is PhD student at CI2MA – University of Concepcion. Subject: Analysis and numerical methods for conservation laws with discontinuous flux and on networks.

At University of Versailles:

Christophe CHALONS  is Professor at the University of Versailles Saint-Quentin-en-Yvelines and Director of the Laboratory of Mathematics. Expertise: Numerical methods for hyperbolic systems of conservation and non conservation laws, applications to compressible multiphase flows and free surface flows.

Past members:

Felisia A. CHIARELLO was PhD student at Inria SAM, EPI ACUMES (Mai 2017 – December 2019). Subject: Conservation laws with non-local flux.

Elena ROSSI was postdoc fellow at Inria SAM, EPI ACUMES (September 2017 – April 2019). Subject: Multi-class traffic flow models.

Camilla FIORINI was PhD student at the Laboratory of Mathematics, University of Versailles Saint-Quentin-en-Yvelines. Subject: Sensitivity analysis for hyperbolic systems with discontinuous solutions.

Rafael ORDONEZ was PhD student at CI2MA – University of Concepcion (July 2017 – January 2021). Subject: Spatio-temporal dynamics of selected multispecies systems: multiclass traffic and predator-prey-taxis models.

Objectives

We aim at designing more efficient numerical algorithms to accurately compute solutions of non-local conservation laws, both by a careful choice of quadrature formulas and the selection of adapted high order methods. In this perspective, we have already obtained encouraging results for scalar equations in 1 space-dimension arising in vehicular traffic and sedimentation modeling.

With this project, we want to extend the study to more general (and computationally expensive) situations of interest in applications, including systems of non-local equations and multidimensional problems. This type of problems arise for example in the modeling of multi-class vehicular traffic, each equation describing the evolution of a given class density, or in models of crowd motion.

Regarding the sensitivity analysis, we aim at extending the results obtained for classical hyperbolic systems , as discontinuous solutions of the Euler equations, to non-local problems. In particular, we will derive the governing equations of the sensitivity variables and define a correction term to be added to the sensitivity equations for these equations to be also valid across discontinuities. In a second time, we will address the construction of numerical schemes with a sharp control of the underlying numerical diffusion. This is a challenging but crucial step to obtain relevant numerical solutions for sensitivities in the context of non-local terms.

Co-funding

  • Fondecyt-Chile Project 1181511 (2018-2021): Modelling and Numerical Analysis for Non-local Systems of Conservation Laws (PI L-M. Villada)
  • Fondecyt-Chile Project 1170473 (2017-2021) (PI R. Burger)
  • MATH-Amsud 22-MATH-05 “NOTION – NOn-local conservaTION laws for engineering, biological and epidemiological applications: theoretical and numerical” (2022-2023) (PI L-M. Villada)

Exchanges

L.-M. Villada visited Inria for 2 weeks in September 2018.

C. Chalons, P. Goatin and L.-M. Villada attended the Workshop WONAPDE in January 2019. In particular,  P. Goatin and L.-M. Villada are the organizers of the mini-symposium “Numerical methods for traffic flow models”.

L.-M. Villada visited Inria for 2 weeks in November 2019.

R. Ordonez visited University of Versailles and Inria for 2 months in November-December 2019.

R. Burger visited Inria for one week in December 2019.

H. Contreras  visited Inria for 2.5 months in October-December 2021.

L.-M. Villada and H. Contreras visited Inria for 2 weeks in June-July 2022.

D. Inzunza visited University of Bio Bio for 1 month in October-November 2022.

Results

2018

During this first year, we have focused on numerical schemes for systems of non-local conservation laws in one space-dimension. In particular, we are concluding the study of Lagrangian-Remap schemes (previously proposed for classical hyperbolic systems) for a non-local multi-class traffic flow model proposed in [F.A. Chiarello, P. Goatin. Non-local multi-class traffic flow models, Netw. Heterog. Media, 14(2) (2019), 371-387.]. The error and convergence analysis show the effectiveness of the method, which is first order, in sharply capturing shock discontinuities and better precision with respect to other methods as Lax-Friedrichs or Godunov (even 2nd order). A journal article about these results is currently in preparation: [F.A. Chiarello, P. Goatin, L.M. Villada. Lagrangian-remap schemes for non-local multi-class traffic flow models. In preparation.]

Truck density computed with different numerical schemes at t=1

Car density computed with different numerical schemes at t=1

A second topic are finite volume methods for non-local multi-class traffic models based on the weighted essentially non-oscillatory (WENO) schemes proposed in [C. Chalons, P. Goatin and L. Villada, High order numerical schemes for one-dimension non-local conservation laws, SIAM J. Sci. Comput., 40 , (2018) pp. A288-A305] in order to obtain high-order shock capturing methods for the non-local multi-class case. A talk based on this topic, titled “High Order Finite-volume Weno Schemes For Non-local Traffic Flow Models” will be presented at WONAPDE 2019 and a work to be presented to the proceedings of the HYP2018 meeting is currently in preparation: [F.A. Chiarello, P. Goatin, L.M. Villada. High Order finite volume schemes for non-local multi-class traffic flow models. In preparation.]

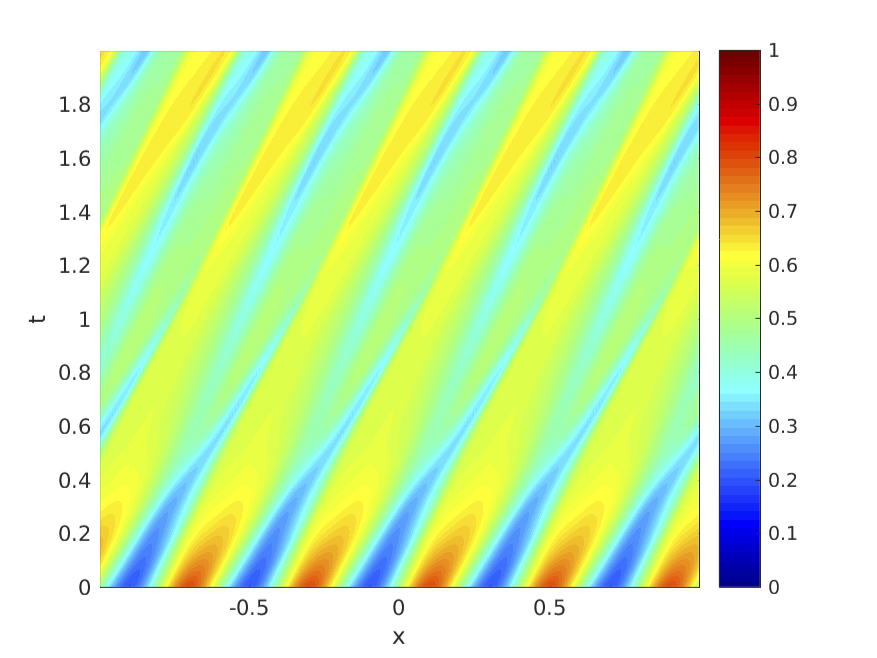
Mixed human driven / autonomous traffic

Fully autonomous traffic

Numerical schemes for convection-diffusion-reaction systems of PDE with non-local flux were proposed, these efficient methods combines Weighted Essentially Non-Oscillatory (WENO) reconstruction and an implicit-explicit Runge-Kutta (IMEX-RK) method for time stepping. The obtained method avoids the restrictive time step limitation of explicit schemes. The following two journal articles about these results are currently accepted: [R. Bürger, D. Inzunza, P. Mulet and L.M. Villada. Implicit-explicit schemes for nonlinear nonlocal equations with a gradient flow structure in one space dimension. to appear in Numer. Meth. Partial Diff. Eqns.] and [R. Bürger, G. Chowell, E. Gavilan, P. Mulet and L.M. Villada. Numerical solution of a spatio-temporal predator-prey model with infected prey. to appear in Math. Biosci. Eng.]

As far as the topic of sensitivity analysis is concerned, we have completed a couple of works devoted to the design of anti-diffusive schemes for systems of conservation laws with local closure relations, in collaboration with C. Chalons, R. Duvigneau and C. Fiorini: [Chalons C., Duvigneau R., Fiorini C. Sensitivity analysis and numerical diffusion effects for hyperbolic PDE systems with discontinuous solutions. The case of barotropic Euler equations in Lagrangian coordinates, to appear in SIAM J. Sci. Comput.] and [Chalons C., Duvigneau R., Fiorini C. Sensitivity equation method for Euler equations in presence of shocks applied to uncertainty quantification, submitted in revised form to Journal of Computational Physics]

2019

We have focused on numerical schemes for systems of non-local conservation laws in one space-dimension. In particular, we have developed a Lagrangian-Remap scheme for a non-local multi-class traffic flow model, which is described and studied in [F.A. Chiarello, P. Goatin, L.M. Villada. Lagrangian-Antidiffusive Remap schemes for non-local multi-class traffic flow models, Comput. Appl. Math., 39, 60 (2020).]

We also developed finite volume methods for non-local multi-class traffic models based on the weighted essentially non-oscillatory (WENO) schemes, which are proposed in [F.A. Chiarello, P. Goatin, L.M. Villada. High Order finite volume WENO schemes for non-local multi-class traffic flow models, in “Hyperbolic Problems: Theory, Numerics, Applications”, AIMS on Applied Mathematics, 10 (2020), 353-560. Proceedings of the XVII international conference in Penn State, June 2018.]

2020

We have revised the non-local macroscopic pedestrian flow model proposed in [R. M. Colombo, M. Garavello, and M. Lécureux-Mercier. A class of nonlocal models for pedestrian traffic. Math. Models Methods Appl. Sci., 22(4):1150023, 2012] to account for anisotropic interactions and the presence of walls or other obstacles in the walking domain. We proved the well-posedness of this extended model and we applied high-resolution numerical schemes to illustrate the model characteristics. In particular, numerical simulations highlight the role of different model parameters in the observed pattern formation. The result are published in [R. Bürger, P. Goatin, D. Inzunza and L.M. Villada. A non-local pedestrian flow model accounting for anisotropic interactions and domain boundaries, Math. Biosci. Eng., 17(5) (2020), 5883-5906.]

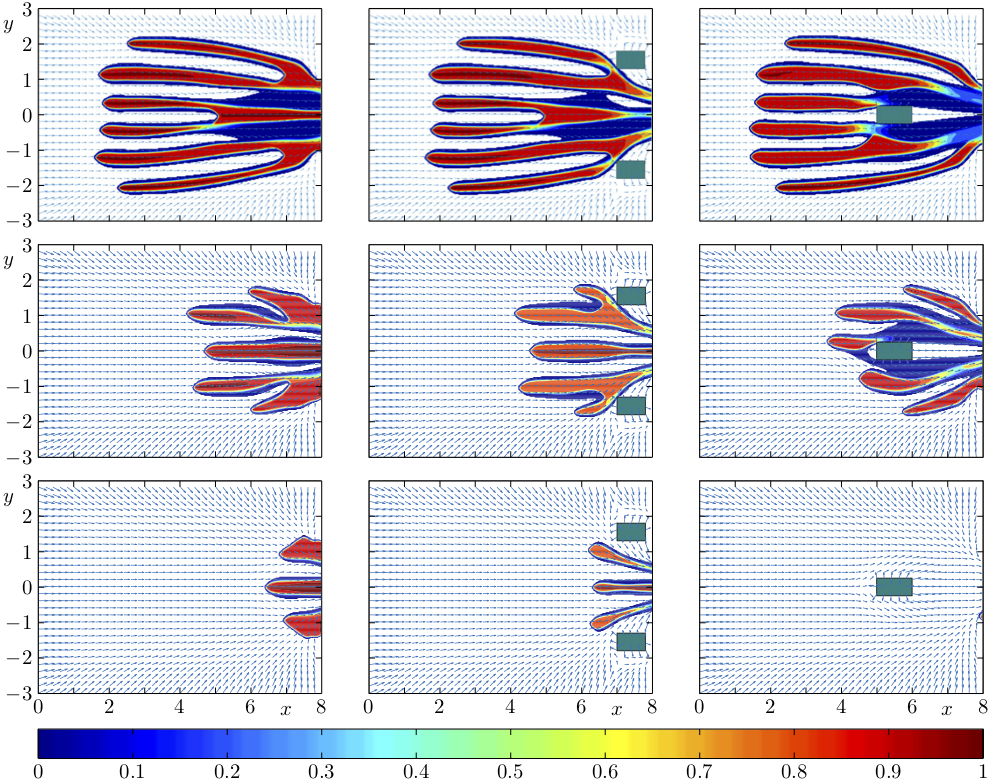
Evacuation of pedestrians corresponding to the different exit designs

Evacuation of pedestrians corresponding to different exit designs

In parallel, we designed a a new numerical scheme to handle flux discontinuities in LWR and multi-class traffic flow models. The scheme is constructed by decomposing the discontinuous velocity function into a Lipschitz continuous function plus a Heaviside function and designing a corresponding splitting scheme. The part of the scheme related to the discontinuous flux is handled by a semi-implicit step that does, however, not involve the solution of systems of linear or nonlinear equations. It is proved that the whole scheme converges to a weak solution in the scalar case. The multi-class scheme satisfies an invariant region principle, that is, all densities are nonnegative and their sum does not exceed a maximum value. In the scalar and multi-class cases no flux regularization or Riemann solver is involved, and the CFL condition is not more restrictive than for an explicit scheme for the continuous part of the flux. The result are presented in [R. Bürger, C. Chalons, R. Ordoñez, L.M. Villada: A multiclass Lighthill-Whitham-Richards traffic model with a discontinuous velocity function, submitted.].

Publications