Félix Miranda-Villatoro web page
e-mail: felix (dot) miranda-villatoro (at) inria (dot) fr
ISFP at TRIPOP team. INRIA Centre at the University Grenoble Alpes, France.
Biography
I am an Electronic Engineer graduated in 2007 from Universidad Autónoma del Estado de México, Mexico. I received the Master and PhD degrees on Automatic Control from Cinvestav-IPN, Mexico in 2013 and 2018, respectively. In 2015, I was a visiting student at BIPOP team in INRIA Grenoble Rhône-Alpes, France. From March 2018 to September 2020, I was a Research Associate in the control group of the University of Cambridge, UK. Since November 2020 I am part of the TRIPOP team where I hold an INRIA Starting Faculty Position at INRIA Centre at the University Grenoble Alpes, France.
-
Non-smooth dynamics
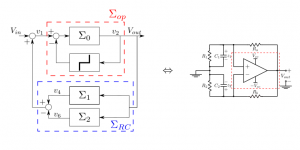 One of the central problems in control theory concerns the design of actions (control laws) that guarantee the regulation of systems. For a control approach to be successful, it must be able to perform well even in the absence of exact knowledge of parameters and under the affections of external disturbances. In this regard, non-smooth controllers (as for instance, non-differentiable, discontinuous, or set-valued maps) are an attractive setting for such a task, since they have robustness properties that cannot be matched by their smooth counterparts.
One of the central problems in control theory concerns the design of actions (control laws) that guarantee the regulation of systems. For a control approach to be successful, it must be able to perform well even in the absence of exact knowledge of parameters and under the affections of external disturbances. In this regard, non-smooth controllers (as for instance, non-differentiable, discontinuous, or set-valued maps) are an attractive setting for such a task, since they have robustness properties that cannot be matched by their smooth counterparts.
Advantages: non-smooth controllers can achieve finite-time convergence, are intrinsically robust against matched uncertainties, and are easy to tune. Additionally, the non-smooth framework is useful for facilitating the modeling stage, as is the case in piece-wise linear and switched systems.
-
Non-equilibrium behaviors
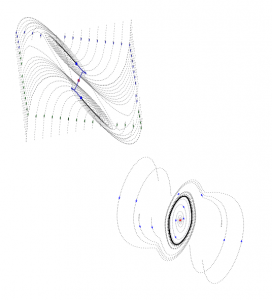 In the context of control and systems, non-equilibrium behaviors arise by nonlinear effects causing local instabilities. Such instabilities are mostly associated to bad design and bad performance in engineering. However, nature is revealing us that non-equilibrium behaviors, such as those observed in switches and oscillators, are at the core of self-organization and robust mechanisms of adaptation. Two properties that are key for survival in our world. The dream of constructing artificial, self-sustained, energy efficient, adaptable systems cannot be fully accomplished without a comprehensive understanding of non-equilibrium behaviors.
In the context of control and systems, non-equilibrium behaviors arise by nonlinear effects causing local instabilities. Such instabilities are mostly associated to bad design and bad performance in engineering. However, nature is revealing us that non-equilibrium behaviors, such as those observed in switches and oscillators, are at the core of self-organization and robust mechanisms of adaptation. Two properties that are key for survival in our world. The dream of constructing artificial, self-sustained, energy efficient, adaptable systems cannot be fully accomplished without a comprehensive understanding of non-equilibrium behaviors.The acknowledge of feedback as the essential modulator of the behavior, at both local and global scales, locates control theory in an exceptional position in the delegation of approaches for a constructive understanding of non-equilibrium behaviors. In this context, extensions of conventional control theory methods, such as Lyapunov theory and dissipitavity theory provide powerful and novel mechanisms for the analysis of such systems.
Publications
Journal Papers
- Younes, A., Miranda-Villatoro, F. A. & Brogliato, B. (2023). Trajectory Tracking in Linear Complementarity Systems with and without State-Jumps: A Passivity Approach. Nonlinear Analysis: Hybrid Systems, 54. [DOI | HAL].
- Miranda-Villatoro, F. A. (2024). Robust output convergence of heterogeneous networks via nonsmooth hard-threshold couplings. Nonlinear Analysis: Hybrid Systems, 52. [DOI | HAL ].
- Miranda-Villatoro, F. A., Castaños F. & Franci, A. (2023). Equivalence of Linear Complementarity Problems: Theory and Application to Nonsmooth Bifurcations, IEEE Transactions on Automatic Control. [DOI | HAL ].
- Perozzi, G., Polyakov, A., Miranda-Villatoro, F. A. & Brogliato B. (2022). Upgrading a linear controller to a sliding mode one: theory and experiments. Control Engineering Practice, 123. [DOI | HAL].
- Miranda-Villatoro, F. A., Forni, F. & Sepulchre, R. (2022). Dissipativity analysis of negative resistance circuits. Automatica, 136. [DOI | arXiv ].
- Miranda-Villatoro, F. A. & Sepulchre, R. (2021). Differential dissipativity analysis of reaction-diffusion systems. Systems and Control Letters, 48. [ DOI | arXiv].
- Miranda-Villatoro, F. A., Castaños, F. & Brogliato, B. (2019). Continuous and discrete-time stability of robust set-valued nested controller, Automatica, 107, 406–417. [ DOI | HAL ]. Nominated by the editor.
- Miranda-Villatoro, F. A., Forni, F. & Sepulchre, R. (2018). Analysis of Lur’e dominant systems in the frequency domain. Automatica, 98, 76–85. [ DOI | arXiv ].
- Miranda-Villatoro, F. A., Brogliato. B. & Castaños, F. (2018). Set-valued sliding-mode control of uncertain linear systems: continuous and discrete time analysis. SIAM Journal on Control and Optimization, 56(3), 1756–1793. [ DOI | HAL ].
- Miranda-Villatoro, F. A., Brogliato, B., & Castaños, F. (2017). Multivalued robust tracking control of Lagrange systems: Continuous and discrete-time algorithms. IEEE Transactions on Automatic Control, 62(9), 4436–4450. [ DOI | HAL ].
- Miranda-Villatoro, F. A., & Castaños, F. (2017). Robust output regulation of strongly passive linear systems with multivalued maximally monotone controls. IEEE Transaction on Automatic Control, 62(1), 238–249. [ DOI | arXiv ].
- Miranda, F. A., Castaños, F. & Poznyak, A. (2016). Min-max piecewise constant optimal control for multi-model linear systems. IMA Journal of Mathematical Control and Information, 33(4), 1157–1176. [ DOI | arXiv ].
Conference Proceedings
- Miranda-Villatoro, F. A. (2024). A dominance approach for the analysis of emergent patterns
in networks. In 11th European Nonlinear Dynamics Conference (ENOC). [ HAL ]. - Miranda-Villatoro, F. A. (2023). Robust synchronization via set-valued maximal monotone couplings. In Proc. of the 21st European Control Conference (ECC), 13-16 [DOI | HAL].
-
Miranda-Villatoro, F. A., Forni, F. & Sepulchre, R. (2018). Dominance analysis of linear complementarity systems. In Proc. of the 23rd International Symposium on Mathematical Theory of Networks and Systems (MTNS), 422–428. [ arXiv ].
-
Miranda-Villatoro, F. A., Forni, F. & Sepulchre, R. (2018). Differentially passive circuits that switch and oscillate. In Proc. of the 2nd IFAC Conference on Modelling, Identification and Control of Nonlinear Systems (MICNON), 19–24. [ DOI | arXiv ].
-
Miranda-Villatoro, F. A., Brogliato, B. & Castaños, F. (2017). Set-valued discrete-time sliding-mode control of uncertain linear systems. In Proc. of the 20th IFAC World Congress. 9607–9612. [ DOI ].
-
Miranda-Villatoro, F. A., Castaños, F. & Brogliato, B. (2017). A set-valued nested controller. In Proc. of the 20th IFAC World Congress. 2971–2976. [ DOI | HAL ].
-
Miranda, F. A. & Castaños, F. (2015). Robust output regulation of linear passive systems using maximally monotone controls. In Proc. of the 54th IEEE Conference on Decision and Control (CDC). 6897–6902. [ DOI ]
-
Miranda, F. A. & Castaños, F. (2014). Robust output regulation of variable structure systems with multivalued controls. In Proc. of the 13th International Workshop on Variable Structure Systems (VSS). 1–6. [ DOI ].
-
Castaños, F., Miranda-Villatoro, F. A., & Franci, A. (2020). A notion of equivalence for linear complementarity problems with application to the design of non-smooth bifurcations. 21st IFAC World Congress 2020. [ arXiv ].
Under review
- Castaños F., Miranda-Villatoro F. A., and Brogliato B. (2024). Multivalued Hamiltonian Systems
with Multivalued Dissipation: Analysis of the Backward-Euler Discretisation. [ HAL ]. - Pham, Q. H., Brogliato, B, and Miranda-Villatoro F. A. (2024). Well-Posedness of Passive Time-
Varying Linear Cone Complementarity Systems. [ HAL ]. - Miranda-Villatoro F. A., Castaños, F. & Brogliato, B., (2024). Finite-time convergent discrete-time algorithms: from explicit to backward schemes. [HAL].
- Miranda-Villatoro, F. A. (2024). A variational approach to the design of discrete-time super-twisting-like algorithms. [HAL].
- Miranda-Villatoro, F. A., Castaños, F. & Brogliato, B. (2023). When proximal-point algorithms meet set-valued systems. An Optimization point of view of discrete-time sliding modes. [HAL].
PhD Thesis
Institution: Automatic Control Department, Cinvestav-IPN, Mexico.
Advisor: Prof. Fernando Castaños Luna
Title: Robust control techniques by using nonsmooth convex analysis tools. [ PDF ].




