May 22, 2015 (2pm) – Euler Violet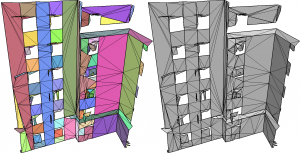
Title: Robust Shape Reconstruction from Defect-Laden Data
Abstract: Surface reconstruction from point clouds is a widely explored problem in geometry processing. Although a high number of reliable methods have been developped over the last two decades, they often require additional measurements such as normal vectors or visibility information. Furthermore, robustness to defect-laden data is only achieved through strong assumptions and remains a scientific challenge.
We focus on defect-laden, unoriented point clouds and propose two new reconstruction approaches designed for two specific classes of output surfaces.
The first method is noise-adaptive and specialized to smooth, closed shapes. It takes as input a point cloud with variable noise and outliers, and comprises three main steps. First, we compute a novel noise-adaptive distance function to the inferred shape, which relies on the assumption that the inferred shape is a smooth submanifold of known dimension. Second, we estimate the sign and confidence of the function at a set of seed points, through minimizing a quadratic energy expressed on the edges of a uniform random graph. Third, we compute a signed implicit function through a random walker approach with soft constraints chosen as the most confident seed points computed in previous step.
The second method generates piecewise-planar surfaces, possibly non-manifold, represented by compact triangle meshes. Through multiscale region growing of Hausdorff-error-bounded convex planar primitives, we infer both shape and connectivity of the input and generate a simplicial complex that efficiently captures large flat regions as well as small features and boundaries. Imposing convexity of primitives is shown to be crucial to both the robustness and efficacy of our approach. We provide a variety of results from both synthetic and real point clouds.




