Dates : 2012 – 2016 Funded : European Research Council Identifier: ERC-StG-2011-277906
Dates : 2012 – 2016 Funded : European Research Council Identifier: ERC-StG-2011-277906
Project Summary Project Publications Project Members
Projection, Learning, and Sparsity for Efficient data processing.
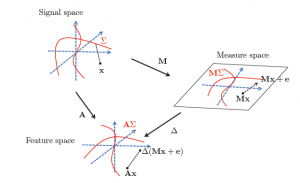
Sparse models are at the core of many research domains where the large amount and high-dimensionality of digital data requires concise data descriptions for efficient information processing. Recent breakthroughs have demonstrated the ability of these models to provide concise descriptions of complex data collections, together with algorithms of provable performance and bounded complexity.
A flagship application of sparsity is the new paradigm of compressed sensing, which exploits sparsity for data acquisition using limited resources (e.g. fewer/less expensive sensors, limited energy consumption, etc.). Besides sparsity, a key pillar of compressed sensing is the use of random low-dimensional projections. While sparse models and random projections are at the heart of many success stories in signal processing and machine learning, their full long-term potential is yet to be achieved.
Some of the sub-topics investigated within PLEASE Project are listed below as clickable links.