Anne Gagneux, PhD student in the team, won the best poster award at the SMAI MODE days 2024, for her M2 internship on “Automatic and unbiased coefficients clustering with non-convex SLOPE”. The poster is available here.
Congratulations Anne!
Apr 09
Best poster prize for Anne Gagneux @SMAI MODE
Mar 19
One paper accepted at SIAM Journal on Imaging Sciences
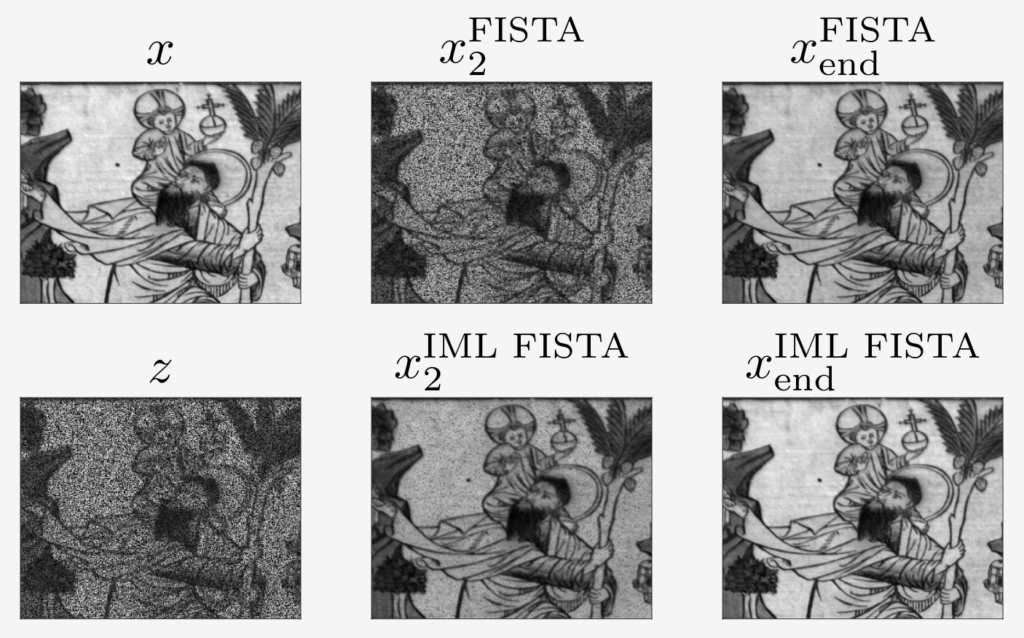
The paper IML FISTA: A Multilevel Framework for Inexact and Inertial Forward-Backward. Application to Image Restoration, by Guillaume Lauga, Elisa Riccietti, Nelly Pustelnik and Paulo Gonçalves, was accepted for publication at SIAM Journal on Imaging Sciences!
This work presents a multilevel framework for inertial and inexact proximal algorithms, that encompasses multilevel versions of classical algorithms such as forward-backward and FISTA.
The methods are supported by strong theoretical guarantees: we prove both the rate of convergence and the convergence of the iterates to a minimum in the convex case, an important result for ill-posed problems.
Several image restoration problems (image deblurring, hyperspectral images reconstruction, etc …) are considered where the proposed multilevel algorithm greatly accelerates the convergence of the one level (i.e. standard) version of the method.
Paper: https://inria.hal.science/hal-04075814
Oct 03
Three papers accepted at NeurIPS 2023
Three papers will be presented this year at NeurIPS in New Orleans.
- Abide by the Law and Follow the Flow: Conservation Laws for Gradient Flows with Sibylle Marcotte, Rémi Gribonval and Gabriel Peyré. Oral presentation.
The purpose of this article to expose the definition and basic properties of “conservation laws”, which are maximal sets of independent quantities conserved during gradient flows of a given model, and to explain how to find the exact number of these quantities by performing finite-dimensional algebraic manipulations on the Lie algebra generated by the Jacobian of the model.
Preprint: https://inria.hal.science/hal-04150576
- Does a sparse ReLU network training problem always admit an optimum? with Quoc-Tung Le, Elisa Riccietti and Rémi Gribonval.
This work shows that optimization problems involving deep networks with certain sparsity patterns do not always have optimal parameters, and that optimization algorithms may then diverge. Via a new topological relation between sparse ReLU neural networks and their linear counterparts, this article derives an algorithm to verify that a given sparsity pattern suffers from this issue.
Preprint: https://inria.hal.science/hal-04108849
- SNEkhorn: Dimension Reduction with Symmetric Entropic Affinities with Hugues Van Assel, Titouan Vayer, Rémi Flamary and Nicolas Courty.
This work uncovers a novel characterization of entropic affinities as an optimal transport problem, allowing a natural symmetrization that can be computed efficiently using dual ascent. The corresponding novel affinity matrix derives advantages from symmetric doubly stochastic normalization in terms of clustering performance, while also effectively controlling the entropy of each row thus making it particularly robust to varying noise levels. Following, it presents a new DR algorithm, SNEkhorn, that leverages this new affinity matrix.
Preprint: https://hal.science/hal-04103326
Jul 06
New preprint “Abide by the Law and Follow the Flow”
New preprint “Abide by the Law and Follow the Flow: Conservation Laws for Gradient Flows” by @SibylleMarcotte, @RemiGribonval and @GabrielPeyre
We define and study “conservation laws” for the optimization of over-parameterized models. https://arxiv.org/abs/2307.00144
Jun 16
6 papers accepted at GRETSI

The following papers will be presented by the team at the next GRETSI:
- “Sparsity in neural networks can improve their privacy“, Antoine Gonon, Léon Zheng, Clément Lalanne, Quoc-Tung Le, Guillaume Lauga, Can Pouliquen. https://hal.science/hal-04062317v2
- “Implicit differentiation for hyperparameter tuning the weighted Graphical Lasso“, Can Pouliquen, Paulo Gonçalves, Mathurin Massias, Titouan Vayer.
- “Méthodes multi-niveaux pour la restauration d’images hyperspectrales“, Guillaume Lauga, Elisa Riccietti, Nelly Pustelnik, Paulo Gonçalves. https://hal.science/hal-04067225v1
- “Factorisation butterfly par identification algorithmique de blocs de rang un“, Léon Zheng, Gilles Puy, Elisa Riccietti, Patrick Pérez, Rémi Gribonval.
- “Scaling is all you need: quantization of butterfly matrix products via optimal rank-one quantization“, Rémi Gribonval, Théo Mary, Elisa Riccietti.
- ”Un algorithme matriciel pour le calcul des composantes connectées d’un réseau complexe temporel”, Rémi Vaudaine, Pierre Borgnat, Paulo Gonçalves, Rémi Gribonval, Márton Karsai.
In addition, Titouan Vayer will organize a special session on “Graph Learning & Learning with Graphs” with Arnaud Breloy.
See you in Grenoble!
Mar 15
Paper accepted at ICLR 2023

We are glad to announce that the paper “Self-supervised learning with rotation-invariant kernels” (Léon Zheng, Gilles Puy, Elisa Riccietti, Patrick Pérez, Rémi Gribonval) has been accepted at the 11th Interanational Conference on Representation Learning (Kigali, May 2023). This project is a collaboration betwen OCKHAM team and valeo.ai.
Oct 27
One paper accepted at Transaction of Machine Learning Research
We are glad to announce that the following paper with contributions from the Dante team have been accepted for publication in the Transaction of Machine Learning Research (TMLR) journal:
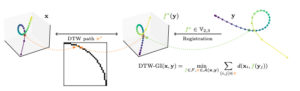
- Time Series Alignment with Global Invariances. Titouan Vayer, Romain Tavenard, Laetitia Chapel, Rémi Flamary, Nicolas Courty, Yann Soullard
Oct 26
Three papers accepted at NeurIPS 2022
We are glad to announce that the following papers with contributions from the Dante team have been accepted for publication at the NeurIPS 2022 conference:
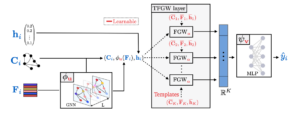
– Template based Graph Neural Network with Optimal Transport Distances, C. Vincent-Cuaz, R. Flamary, M. Corneli, T. Vayer & N. Courty.
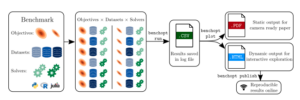
– Benchopt: Reproducible, efficient and collaborative optimization benchmarks, T. Moreau, M. Massias, A. Gramfort and others.
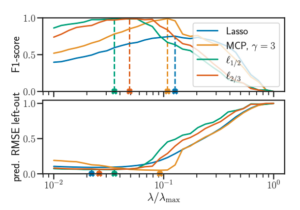
– Beyond L1: Fast and better sparse models with skglm, Q. Bertrand, Q. Klopfenstein, P.-A. Bannier, G. Gidel & M. Massias
Oct 10
Paper accepted for publication in SIMODS
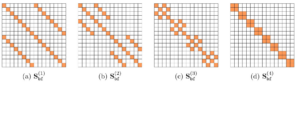 We are pleased to announce that our work “Efficient Identification of Butterfly Sparse Matrix Factorizations” (Léon Zheng, Elisa Riccietti, Rémi Gribonval) has been accepted for publication in SIAM Journal on Mathematics of Data Science.
We are pleased to announce that our work “Efficient Identification of Butterfly Sparse Matrix Factorizations” (Léon Zheng, Elisa Riccietti, Rémi Gribonval) has been accepted for publication in SIAM Journal on Mathematics of Data Science.
This work studies identifiability aspects of sparse matrix factorizations with butterfly constraints, a structure associated with fast transforms and used in recent neural network compression methods for its expressiveness and complexity reduction properties. In particular, we show that the butterfly factorization algorithm from the article “Fast learning of fast transforms, with guarantees” (ICASSP 2022) is endowed with exact recovery guarantees.