Participants:
Sébastien Benzekry, Clair Poignard and Olivier Saut
Biology labs involved:
Angiogenesis and cancer microenvironment laboratory, Inserm, Bordeaux, directed by the Pr Andreas Bikfalvi.
John Ebos’s laboratory, Roswell Park Cancer Institute, Buffalo, NY, USA.
In order to gain biological understanding of complex phenomena, we develop theoretical mathematical models for various processes of cancer biology such as avascular and vascular tumor growth but also development of a cancer disease at the organism level, integrating the metastatic process (which represents the major cause of death in a cancer disease). These models yield insights about various topics including anti-angiogenic therapies, metastatic dormancy or post-surgery metastatic acceleration.
Metastatic dynamics, impact of surgery and tumor-tumor interactions
-
- Mathematical modeling of metastatic development and effect of surgery
In collaboration with John Ebos, we develop numerical tools for the analysis of in vivo bioluminescence data of metastatic development in clinically relevant animal models (i.e., including surgery, post-surgery spontaneous metastatic growth and adjuvant therapy.) This adds a rational and formal component to the mere statistical analysis of the data.
- Mathematical modeling of metastatic development and effect of surgery
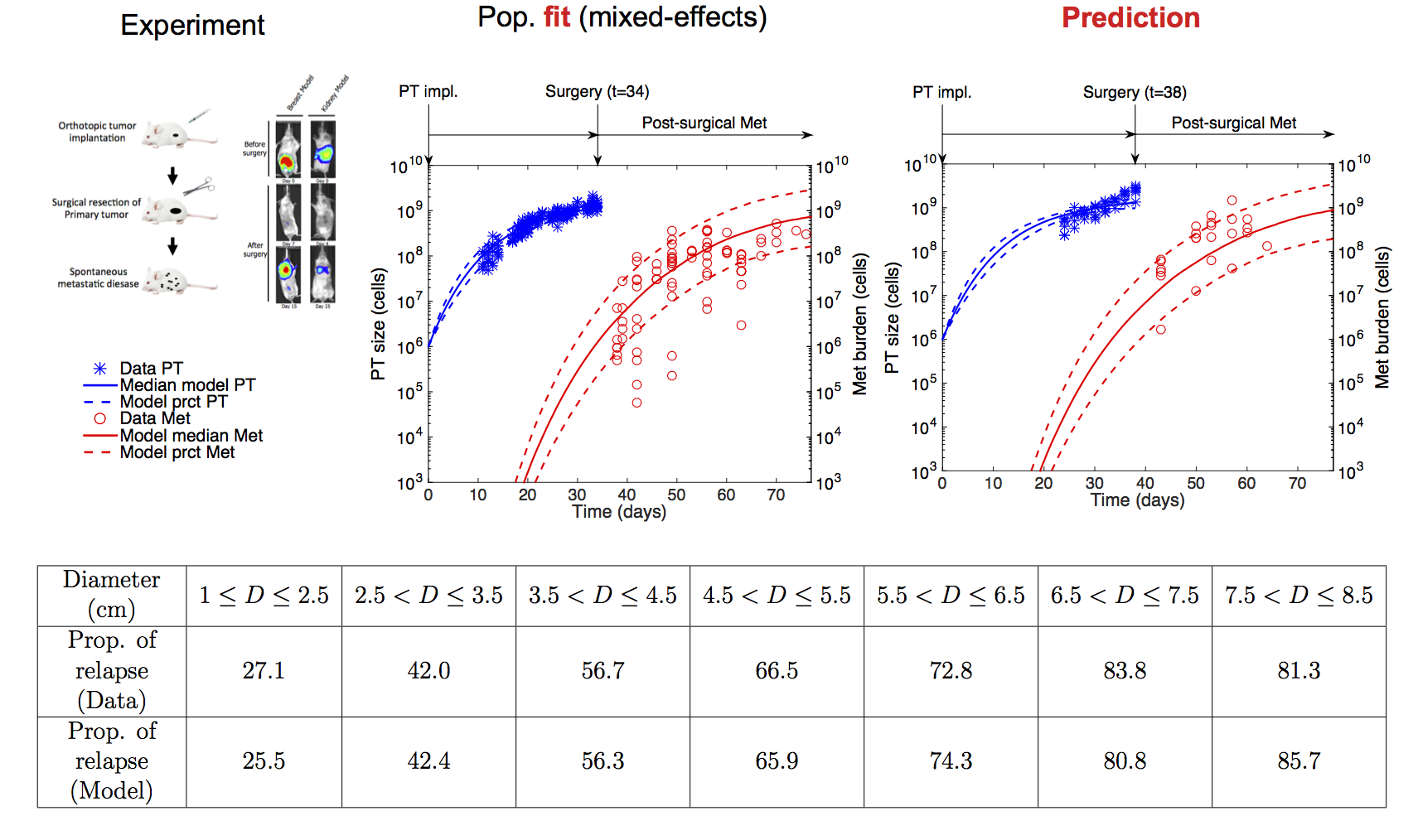
Figure: Top row: Preclinical data. Left: Experimental setting for non-invasive monitoring of metastatic development in an orthotopic (= at the original site, i.e. the mammary fat pad for breast cancer and the kidney for renal cancer) and clinically relevant animal models of breast and kidney cancer metastases. Data from John Ebos’s lab (Roswell Park Cancer Institute, Buffalo, NY, USA). Middle: Population fit of the breast data set, based on a semi-mechanistic model for description of the population of metastases and nonlinear mixed-effects statistical framework for parameters estimation. Right Prediction of an independent data set, where surgery was performed at a different time. PT = Primary Tumor. Met = Metastatic burden. Bottom row: Fit of clinical data of metastatic relapse probability for 2648 breast cancer patients (data from Koscielny et al., Br J Cancer, 1984) using the same model developed in the preclinical phase
Movie: Simulation of the cancer history of a virtual patient with high metastatic potential. In grey are the metastases that appeared before the detection (and subsequent resection) of the primary lesion, that was simulated here to be detected when reaching a diameter of 4 centimeters. In white, the metastases that would have occurred if the primary tumor had not been removed.
-
- Systemic inhibition of angiogenesis, global dormancy and post-surgery metastatic acceleration
In collaboration with the Center of Cancer and Systems Biology in Boston (in particular with Philip Hahnfeldt), we study angiogenic tumor-tumor interactions and the implications for global dynamics of a cancer disease combining biological experiments and quantitative modeling. Indeed, tumors are known to relase in the circulation anti-angiogenic molecules that provoke Systemic Inhibition of Angiogenesis (SIA) and collectively suppress the growth of all lesions. Models are written at the organism scale, taking into account both primary and secondary tumors (metastases). Clinical and biological implications of the SIA theory for metastatic global dormancy (“Cancer without disease”) and possible acceleration of metastatic growth after removal of a primary lesion are derived.
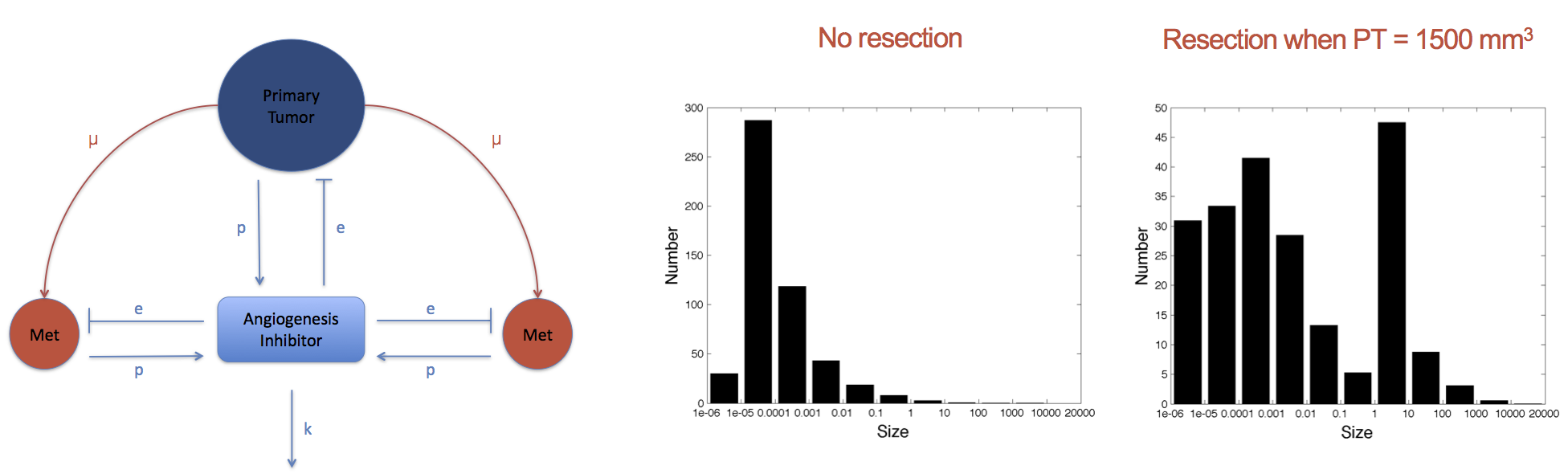
Figure: A model for systemic inhibition of angiogenesis and simulation reproducing an experiment with resection or not of primary tumor when it reaches 1500 mm3. Size distribution of the metastases at the end shows growth acceleration of preexisting metastases.
-
- Metastatic initiation and influence of the micro-environment
Based on biological experiments performed in the Angiogenesis and cancer microenvironment laboratory, we used mathematical modelling to formalize the standard theory of metastatic initiation, under which secondary tumours, after establishment in a distant organ, grow independently from each other and from the primary tumour. When calibrated on the experimental data of primary tumour and total metastatic burden in the lungs in an animal model of renal cell carcinoma, the initial model predicted a size distribution of metastatic foci that did not fit with observations obtained experimentally using magnetic resonance imaging (which provided size and number of macro-metastases). The model predicted an increase in the number of lesions, but of smaller size when compared to the data. This led us to revise the standard theory and to propose two hypotheses in order to explain the observations: 1) small metastatic foci merge into larger ones and/or 2) circulating tumour cells may join already established tumours. We then derived a spatial model of tumour growth in order to explore the quantitative implications of tumours merging on global tumour growth and estimated the numbers of required metastatic foci to obtain the observed metastatic volumes. For more details, see Baratchart et al., Computational modelling of metastasis in renal cell carcinoma, PloS Comput Biol, 2015.
Left: Simulation of a lung metastasis starting from the shape of the segmented metastatic focus on MRI image. Middle: Simulation of two neighboring tumors are growing and pushing each other by passive motion. Right: Simulation of merging metastatic foci. See Baratchart et al., Computational modelling of metastasis in renal cell carcinoma, PloS Comput Biol, 2015.
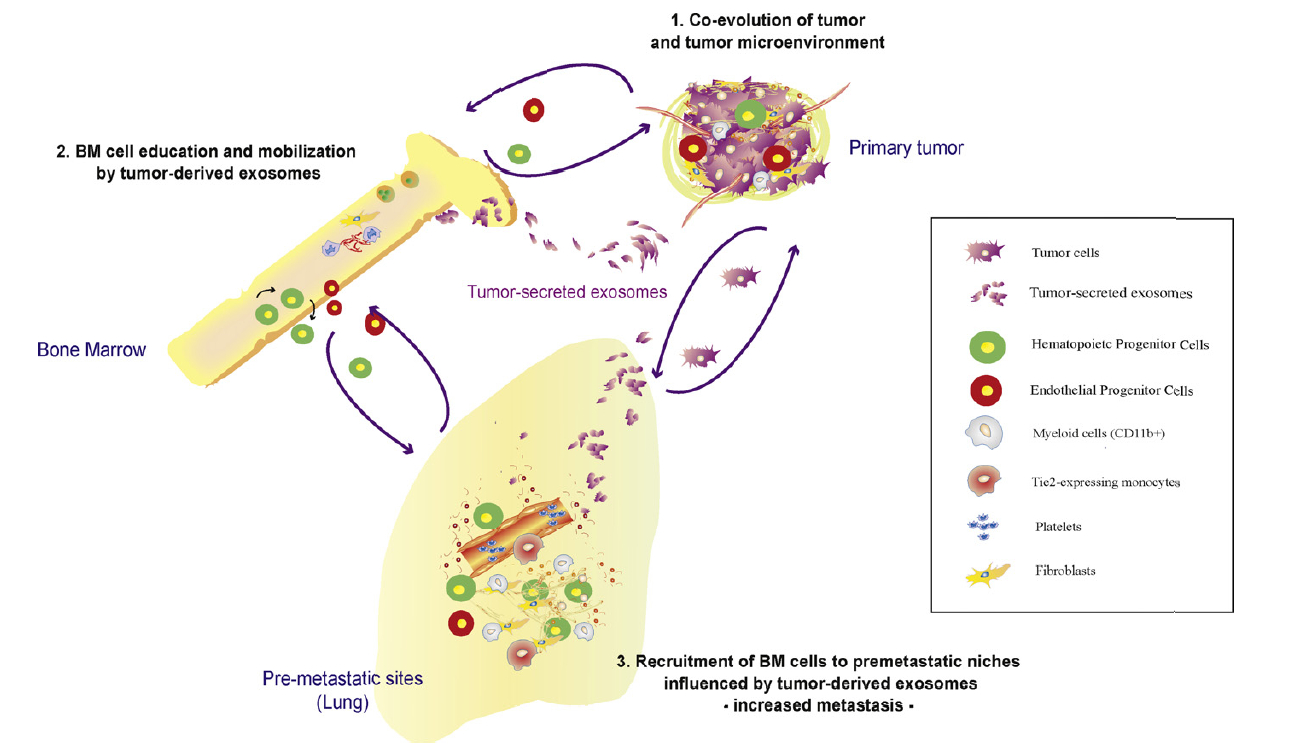
We are also interested in the theory of the pre-metastatic and metastatic niche. These are newly discovered biological processes by which a pre-established primary tumor prepares the soil in distant organs for seeding of migratory cells that develop into metastases. Activation of distant stroma such as fibroblast cells is thought to be mediated by bone-marrow derived cells recruited by cytokines emitted by the primary tumor. By establishing and validating a mathematical model, we want to identify critical players in this phenomenon in order to help to develop anti-metastatic strategies.
Theoretical models of tumor growth
In a series of work together with B. Ribba and E. Grenier we have introduced a generic PDE (partial differential equations) model for tumor growth. The models were designed for both vascular and avascular stages. The model is based on the description of the development of populations of cells. We consider proliferative cells, quiescent cells and healthy tissues. The proliferative cells undergo a cell cycle that is regulated by various biological processes such as hypoxia or overcrowding.
The distribution of oxygen depends on a vascular network that is obtained through an angiogenesis model that describes proliferation and migration of endothelial cells according to chemotaxis phenomena regulated by secretion of several pro- and anti-angiogenic factors (VEGF, PDGF, angiostatin, angiopoietin,…). Interaction with the extracellular matrix and influence of metalloproteinases are also considered. Several mechanical aspects have been investigated (visco-elasticity, elasticity of membranes, Darcy’s law, …). Eventually, we have also tested the influence of several treatments (radiotherapy, chemotherapy, anti-angiogenic drugs, inhibitors of MMP…). The model has been implemented in a 3D framework in C++ in the platform developed by O. Saut.

