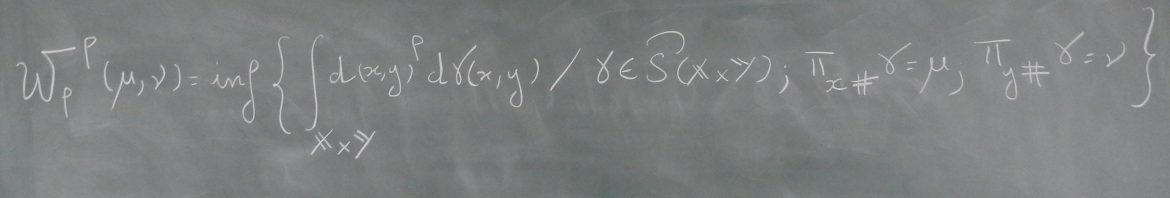INRIA PARIS 10h30 Salle JLL
Francis Bach (SIERRA) [SLIDES]
Title: Submodular Functions: from Discrete to Continous Domains
Résumé: Submodular set-functions have many applications in combinatorial optimization, as they can be minimized and approximately maximized in polynomial time. A key element in many of the algorithms and analyses is the possibility of extending the submodular set-function to a convex function, which opens up tools from convex optimization. Submodularity goes beyond set-functions and has naturally been considered for problems with multiple labels or for functions defined on continuous domains, where it corresponds essentially to cross second-derivatives being nonpositive. In this paper, we show that most results relating submodularity and convexity for set-functions can be extended to all submodular functions. In particular, (a) we naturally define a continuous extension in a set of probability measures, (b) show that the extension is convex if and only if the original function is submodular, (c) prove that the problem of minimizing a submodular function is equivalent to a typically non-smooth convex optimization problem, and (d) propose another convex optimization problem with better computational properties (e.g., a smooth dual problem). Most of these extensions from the set-function situation are obtained by drawing links with the theory of multi-marginal optimal transport, which provides also a new interpretation of existing results for set-functions. We then provide practical algorithms to minimize generic submodular functions on discrete domains, with associated convergence rates. (available at https://hal.archives-ouvertes.fr/hal-01222319v2/document)
Bernhart Schmitzer (MOKAPLAN)
Title: A Stabilized Sparse Sinkhorn Algorithm
Abstract: Sinkhorn’s matrix scaling algorithm is a simple way to solve entropy regularized optimal transport problems. It is almost trivial to implement, apt for parallelization and relatively fast for large to moderate regularization strength. However, as regularization becomes smaller, it takes an increasing number of iterations to converge and becomes numerically unstable due to the limited precision of floating point variables. Moreover, as the problem size increases, it becomes increasingly expensive to compute convolutions with the dense matrix kernel, and it may even become impossible to store the full kernel in memory. We propose a number of adaptations to the algorithm to overcome the limitations of small regularization and large problems: log-domain parametrization of the scaling factors, gradual decreasing of the regluarization parameter, and a hierarchical multi-scale scheme with sparse sub-sampling of the kernel. It turns out that the adaptations work best, when applied in careful combination.