Topological Data Analysis
Topological Data Analysis (TDA) is a recent field that emerged from various works in applied (algebraic) topology and computational geometry during the first decade of the century. TDA is mainly motivated by the idea that topology and geometry provide a powerful approach to infer robust qualitative, and sometimes quantitative, information about the structure of data. Its overall goal is two-fold. First, TDA aims at providing mathematical results and methods to infer, analyze and exploit the complex topological and geometric structures underlying data that are often represented as point clouds in Euclidean or more general metric spaces. Second, it intends to give access to robust and efficient data structures and algorithms to represent these data and that are amenable to precise analysis.
Many important advances have been made in TDA during the last decade leading to applications in various fields.
However, TDA is still facing important challenges that need to be addressed. So far the existing results and methods rely mostly on deterministic assumptions which often lead to tools that are sensitive to noise and outliers, remain exploratory and do not benet from a sound probabilistic framework. Despite a few notable promising attempts to overcome this problem, the development of a statistical approach to TDA is still in its infancy. On the algorithmic side, as data are becoming larger and larger, both in size and dimension, the design and analysis of geometric data structures and algorithms are of fundamental importance. Computational topology and geometry have been successful in the development of efficient geometric data structures and algorithms in low dimensional spaces, and there is now a real need to go beyond.
Research Directions
Algorithmic aspects of topological and geometric data analysis
TDA requires to construct and manipulate appropriate representations of complex and high dimensional shapes. A major difficulty comes from the fact that the complexity of data structures and algorithms used to approximate shapes rapidly grows as the dimensionality increases, which makes them intractable in high dimensions. We focus our research on simplicial complexes which offer a convenient representation of general shapes and generalize graphs and triangulations. Our work includes the study simplicial complexes with good approximation properties and the design compact data structures to represent them.
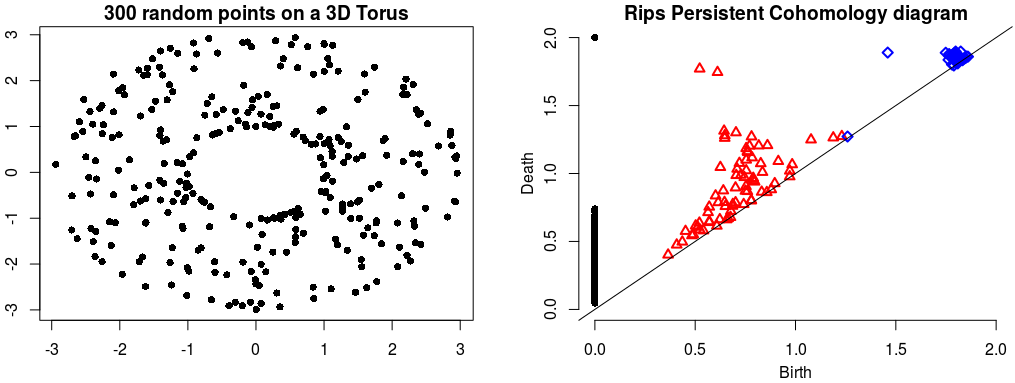
In low dimensions, effective shape reconstruction techniques exist that can provide precise geometric approximations very efficiently and under reasonable sampling conditions. Extending those techniques to higher dimensions as is required in the context of TDA is problematic since almost all methods in low dimensions rely on the computation of a subdivision of the ambient space. A direct extension of those methods would immediately lead to algorithms whose complexities depend exponentially on the ambient dimension, which is prohibitive in most applications. A first direction to by-pass the curse of dimensionality is to develop algorithms whose complexities depend on the intrinsic dimension of the data (which most of the time is small although unknown) rather than on the dimension of the ambient space. Another direction is to resort to cruder approximations that only captures the homotopy type or the homology of the sampled shape. The recent theory of persistent homology, pro- vides a powerful and robust tool to study the homology of sampled spaces in a stable way.
Statistical aspects of topological and geometric data analysis
The wide variety of larger and larger available data – often corrupted by noise and outliers – requires to consider the statistical properties of their topological and geometric features and to propose new relevant statistical models for their study.
There exist various statistical and machine learning methods intending to uncover the geometric structure of data. Beyond manifold learning and dimensionality reduction approaches that generally do not allow to assert the relevance of the inferred topological and geometric features and are not well-suited for the analysis of complex topological structures, set estimation methods intend to estimate, from random samples, a set around which the data is concentrated. In these methods, that include support and manifold estimation, principal curves/manifolds and their various generalizations to name a few, the estimation problems are usually considered under losses, such as Hausdorff distance or symmetric difference, that are not sensitive to the topology of the estimated sets, preventing these tools to directly infer topological or geometric information. Regarding purely topological features, the statistical estimation of homology or homotopy type of compact subsets of Euclidean spaces, has only been considered recently, most of the time under the quite restrictive assumption that the data are randomly sampled from smooth manifolds.
In a more general setting, with the emergence of new geometric inference tools based on the study of distance functions and algebraic topology tools such as persistent homology, computational topology has recently seen an important development offering a new set of methods to infer relevant topological and geometric features of data sampled in general metric spaces. The use of these tools remains widely heuristic and until recently there were only a few preliminary results establishing connections between geometric inference, persistent homology and statistics. However, this direction has attracted a lot of attention over the last three years. In particular, stability properties and new representations of persistent homology information have led to very promising results that open many perspectives and research directions that need to be explored.
We work on the development of the mathematical foundations of Statistical Topological and Geometric Data Analysis. Our ultimate goal is to provide a well-founded and effective statistical toolbox for the understanding of topology and geometry of data.
Topological approaches for multimodal data processing
Due to their geometric nature, multimodal data (images, video, 3D shapes, etc.) are of particular interest for the techniques we develop. Our goal is to establish a rigorous framework in which data having different representations can all be processed, mapped and exploited jointly. This requires adapting our tools and sometimes developing entirely new or specialized approaches.
The choice of multimedia data is motivated primarily by the fact that the amount of such data is steadily growing (with e.g. video streaming accounting for nearly two thirds of peak North-American Internet traffic, and almost half a billion images being posted on social networks each day), while at the same time it poses signi cant challenges in designing informative notions of (dis)-similarity as standard metrics (e.g. Euclidean distances between points) are not relevant.
Software
We are working on datastructures to represent complexes that encode the data, with tools to extract those complexes from data. We are also working on algorithms to sample, mesh and reconstruct manifolds, and others to compute persistent homology, clusters and signatures.
Software is made available mostly through the libraries CGAL, for low dimensions and where arithmetic robustness is key, and GUDHI, for more combinatorial and topological developments (see section Software).
Transfer and applications
