The following figures and movies illustrate the bifurcations observed in the retinal waves model proposed in [1],[2],[3] when moving in the two dimensional bifurcation map in the parameters space GS, GA (see below and Fig. 1 of [3]). Click on the figures to have a better resolution.
I. Global bifurcation map
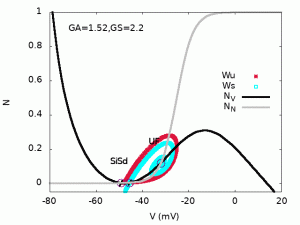
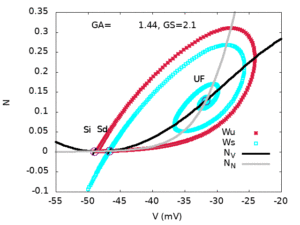
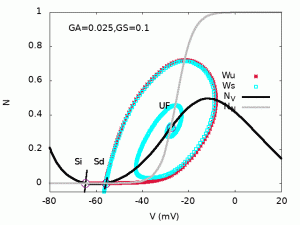
”SN” stands for ”Saddle-Node bifurcation”, ”Hc” for ”Homoclinic bifurcation”, ”Hopf” for ”Hopf bifurcation”, ”SNIC” for ”Saddle-Node on an Invariant Cycle”,”SNH” for Saddle-Node-Homoclinic point (also called saddle-node separatrix loop[4], SNSL), ”BT” stands for Bogdanov-Takens. At the SNH codim-2 bifurcation point, there is a Hc bifurcation line connecting to the BT point with a SNIC emerging from the opposite side of the SNH in which the SN2 and Hc are tangent. At the BT point, there is, on one side the SN1 line and, on the other side the Hc, the SN1 and a Hopf line, tangent at the BT point (see zoom below). Inset: Zoom on region D, in log scale. The Hc and SN2 line meet tangentially at the SNH point and a SNIC line emerges on the other side. The side panels represent phase portraits in regions A, B, D, C with nullclines (NV , in black, is the V nullcline, NN , in grey, is the N nullcline), stable manifold of hyperbolic fixed points (Ws in cyan), unstable manifold of the saddle-fixed points (Wu in red), stable periodic orbit (in blue). ”Si” means ”Sink”, ”Sd” means ”Saddle”, ”UF” means ”Unstable Focus”, ”SPo” means ”Stable Periodic orbit”.
Pathways. The following movies displays the changes in the phase portrait of the model when moving along the corresponding pathways.
- Crossing the SNIC bifurcation line (in green dashed) at GS=2.2 for increasing GA (SNIC bifurcation).
Note that the unstable manifold shrinks to 0 because simulations are run for a fixed time independent on parameters value. When approaching the bifurcation line the characteristic time decreases and it takes longer to observe the whole unstable manifold.
- Crossing region D when GS=0.1 for increasing GA.
One switches from a phase portrait with one sink (Si), one saddle (Sd) and one unstable Focus (region A) to a phase portrait with one sink (Si), one saddle (Sd) and one unstable Focus and a stable limit cycle by homoclinisation (Hc) at GA=0.028. Then Si and Sd merge by a saddle-node bifurcation (SN1 line) at GA=0.055 such that the phase portrait has only a stable limit cycle left.
II. Zoom in the Bogdanov-Takens-Cusp region. Click on the figures to have a better resolution.
Legend. When increasing GS , the SNIC line (in green) gives rise, at the Saddle-Node-Homocline point (SNH, located at GS = 2.25, GA = 1.58) to a Saddle-Node line (SN2 , in brown) and to a Homoclinic curve (blue points). This homoclinic curve terminates at the Bogdanov-Takens point (BT, located at GS = 2.59, GA = 1.68) where it meets a Saddle-Node line (SN1 in blue). At this point a Hopf bifurcation line starts (in orange). The two Saddle-Node lines SN1, SN2 meet at the cusp point located at GS = 3.21, GA = 2.566
Pathways. The following movies displays the changes in the phase portrait of the model when moving along the corresponding pathways.
1.
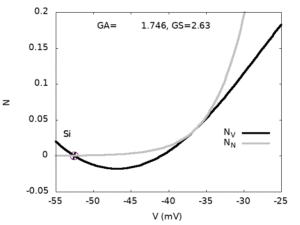
A SN bifurcation, at GA=1.748, is followed by a Hopf creating a limit cycle at GS=1.756 (in the movies this corresponds to change in the stability of the Stable Focus to an unstable one, but the cycle is not visible being too small. It becomes visible at GS=1.76). The cycle disappears by homoclinisation at GS=1.774 and reappears, again by homoclinisation at GS=1.885. Finally, the Si and the Sd merge at by GS=1.942 leaving the stable limit cycle alone (region C).
2.
The Sd and Si meet at the SNIC line, giving rise to stable limit cycle.
Bibliography.
[1] D. Karvouniari, L. Gil, O. Marre, S. Picaud, B.Cessac. A biophysical model explains the spontaneous bursting behavior in the developing retina, Scientific Reports, Nature Publishing Group, 2019, 9 (1), pp.1-23. [2] D. Karvouniari, Retinal waves : theory, numerics, experiments, PhD thesis [3] B. Cessac, D. Matzakou-Karvouniari, The non linear dynamics of retinal waves, submitted [4] S. Schecter. The saddle-node separatrix-loop bifurcation. SIAM J. Math. Anal., 18:1142–1157, 1987.