The version #6 of our latest report is now available:
On an interval prediction of COVID-19 development based on a SEIR epidemic model
https://hal.inria.fr/hal-02517866
In this report, a revised version of the well-known mathematical outbreak SEIR model is used to analyze the epidemic’s course of COVID-19 in eight different countries. The proposed model enhancements reflect the societal feedback on pandemic and confinement features. The parameters of the SEIR model are identified by using publicly available data for France, Italy, Spain, Germany, Brazil, Russia, New York State (US), and China. The identified model is then applied for the prediction of the SARS-CoV-2 virus propagation under different conditions of confinement. For this purpose, an interval predictor is designed allowing variations and uncertainties in the model parameters to be taken into account. The code and the utilized data are available in Github.
The objective of this research is simply to give an intuition of the possible evolution of COVID-19 epidemics. The selected model is fairly basic, allowing the parameters to be identified from the data, while the interval framework expands its forecasting capacities in the face of uncertainties. The suggested model improvements are oriented on modelization of the confinement and the societal feedback influences on the outbreak development.
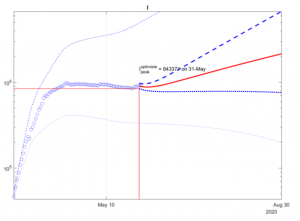
For example, the results of interval prediction of the number of active infected individuals for France give the following:
where the results are plotted in logarithmic scale,
- blue circles represent the recorded values in the past;
- blue dash and dot lines show the interval predictions originated from the current state under admissible variations of parameter values (upper and lower ones are pessimistic and optimistic forecasts, respectively);
- red line corresponds to the model behavior in future starting from today’s data.
As we can conclude, in the optimistic setting the peak of outbreak has been passed already.