Cartesian and Octree meshes
Modelling multi-scale physical phenomena usually involves the capability of describing geometrical features of different sizes and strong variations of the variables in a small portion of the computational domain. In these cases, the use of grids with the same global resolution could be an unaffordable numerical challenge even in a HPC framework.
In order to reduce the computational cost and the memory footprint, we chose to discretize the model equations on adaptive meshes. Among this kind of grids, quadtrees/octrees allow not only a strong reduction of the number of degrees of freedom where the problem exhibit smooth behaviour or smooth geometrical features, but also a strongly localized increase of information in areas needing more accuracy. In particular, the linear octrees introduce a simple structure easy to be implemented for parallel computing applications.
Fig 1 Example of 3D mesh refinement around a surface using a linear octree.
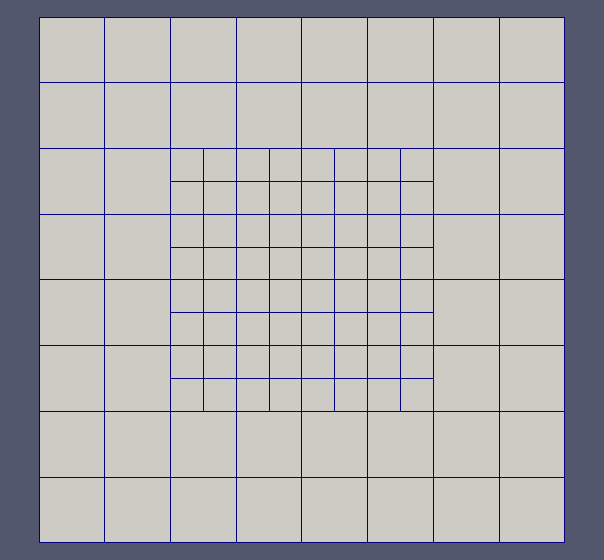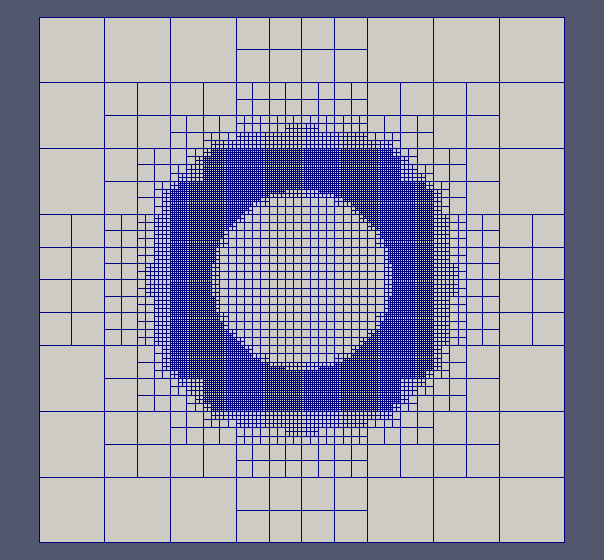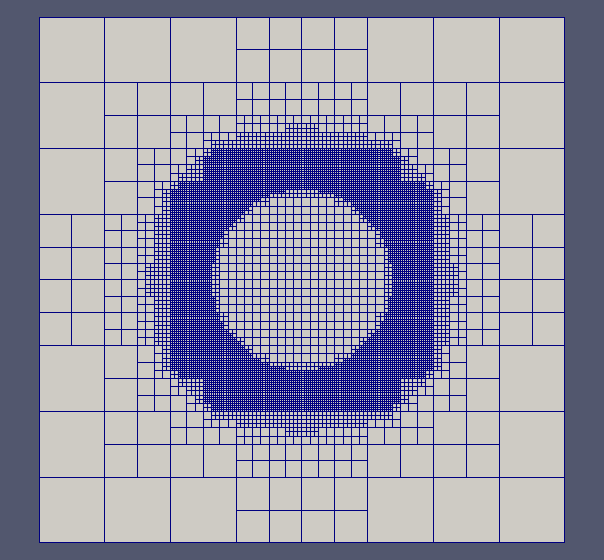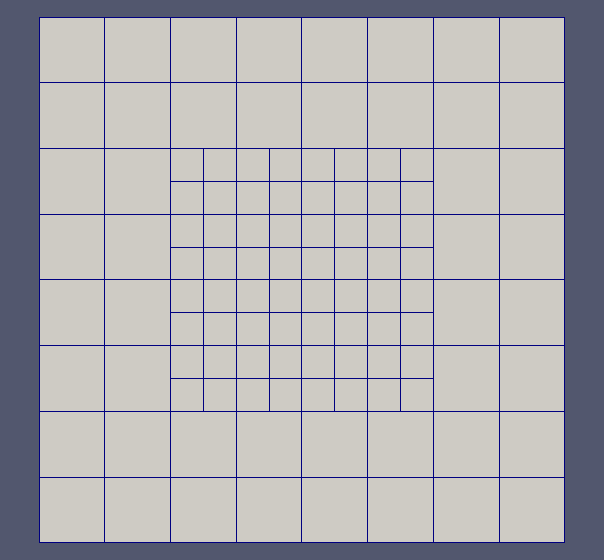
Fig 2 Example of an adaptive adapting involving several refinements inside a circle and successive coarsening a smaller circle.
Our team contributes to the development of a software library to manage parallel load balanced linear quadtrees/octrees, called PABLO. This library, embedding Message Passage parallelism, allows the user to implement his/her methods on this kind of grids, avoiding the burden of explicitly dealing with parallel communications.
The use of these grids involves the need for new schemes able to manage the non-conformity naturally introduced by local adaptation.
We started focusing on elliptic problems because of their widespread presence in the models developed by our team. Both the finite difference method and the finite volume method are used to study two different numerical schemes.
The finite difference scheme consists of cell-centered scheme built in order to ensure the local consistency and to get as close as possible a global second order error. This approach is based on the identification of all possible cell neighbours patterns on a graded mesh and on the computation of finite difference coefficients for each of these configurations.
Some test cases, using complex locally refined meshes, have been studied to prove the convergence to the solution. The scheme exhibits a global error convergence rate of 1.4. Some other tests have been performed introducing the penalisation method; in this case the scheme has been proved to have a first order error convergence rate as expected. (In figures different examples of relative applications)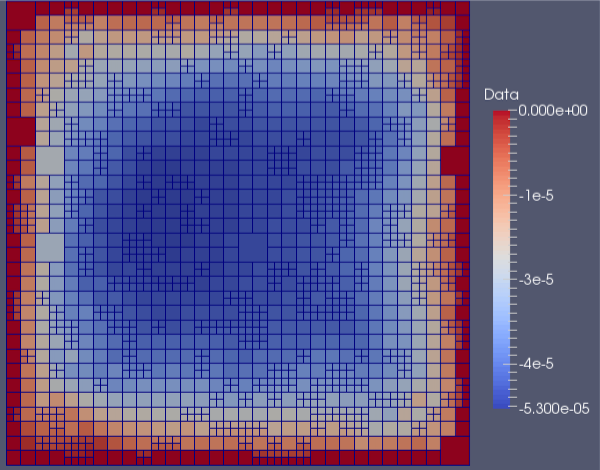
Fig 3. Laplacian resolution on a random mesh: error distribution.
As in the previous approach, the finite volume scheme is intended for graded non-conformal grids, at least at the moment. Given the weak formulation of the elliptic problem, we compute the cell gradients using a least square method, minimizing a second order reconstruction of the solution in the cell neighbours; the gradients at the surface of the cell are evaluated by a weighted average of the gradients in the cells sharing that surface; therefore, a finite difference correction is introduced along the direction connecting the involved cell centers and the sum of cell fluxes is computed.
For the first test cases we studied, this scheme exhibits a second order error convergence in all the considered norms.
Both the schemes are used to numerical simulate the behaviour of two different classes of materials: phase changing materials to store thermal energy and electrostrictive materials for electric energy production. In these problems the both geometry and physical behaviour require high mesh resolution in localized areas of the domain giving the grid adaptation an important role in the simulation feasibility .
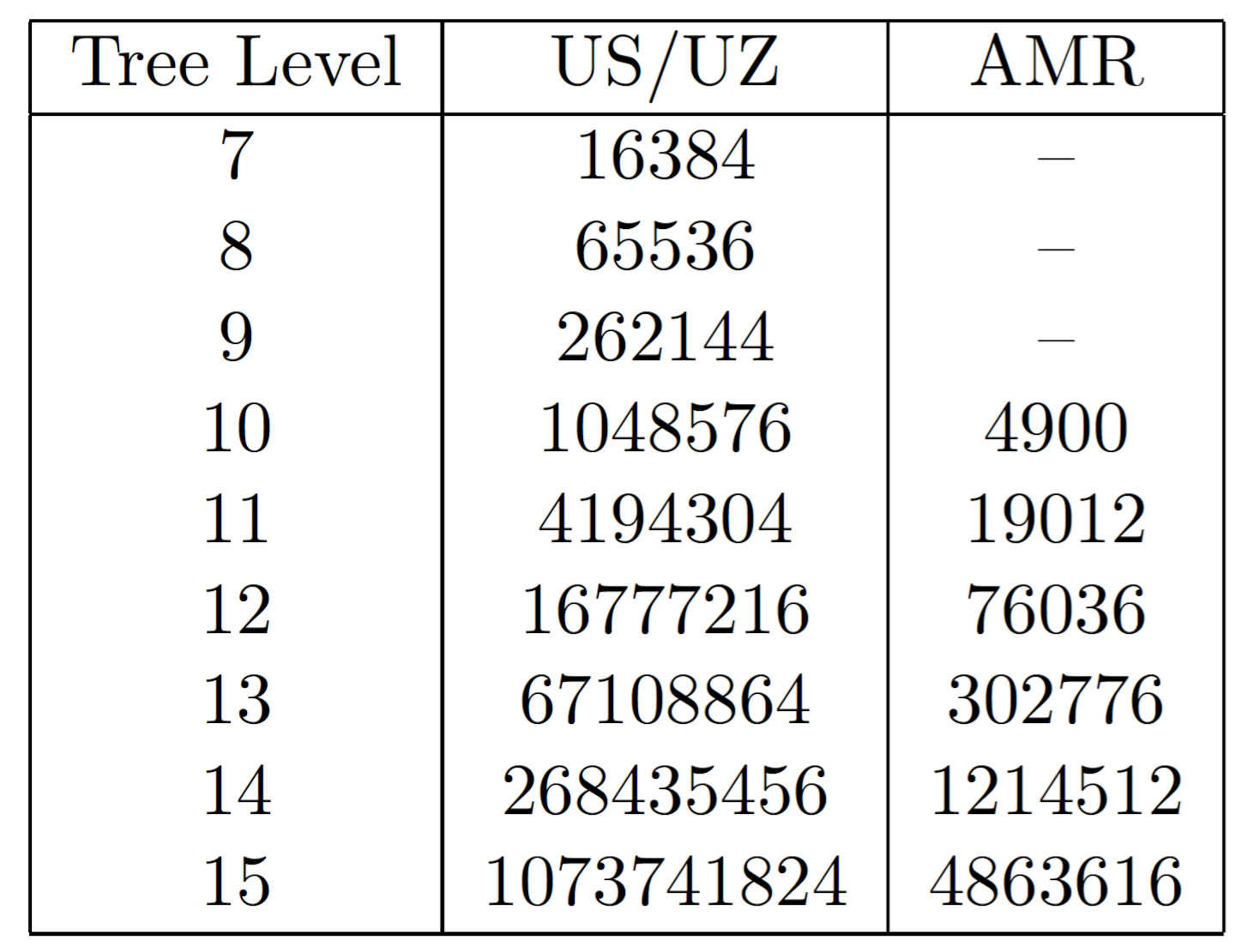
Uniform renement and AMR for a multi scale problem
The finite difference method has been compared also with Cartesian uniform grids. We investigate an idealized multiscale problem with the same domain and exact solution as in previous sections, but we now we consider a penalization domain inside a centered cylinder with radius 0,01.
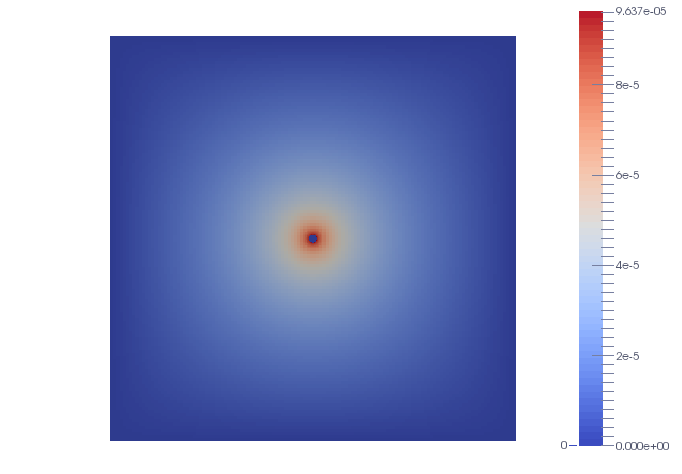
Fig 4. Penalization around a circle of radius 0,01: error distribution.
We could evidence the gain in terms of degrees of freedom, thus in memory. To valid the method also three dimensional cases have been proposed.
Three dimensional extensions
Fig 5. Residual distribution of three dimensional laplacian operator.
The finite method has been validated in three dimension, we studied the residual operator convergence and we repeated the two dimensional tests proving the convergence order.
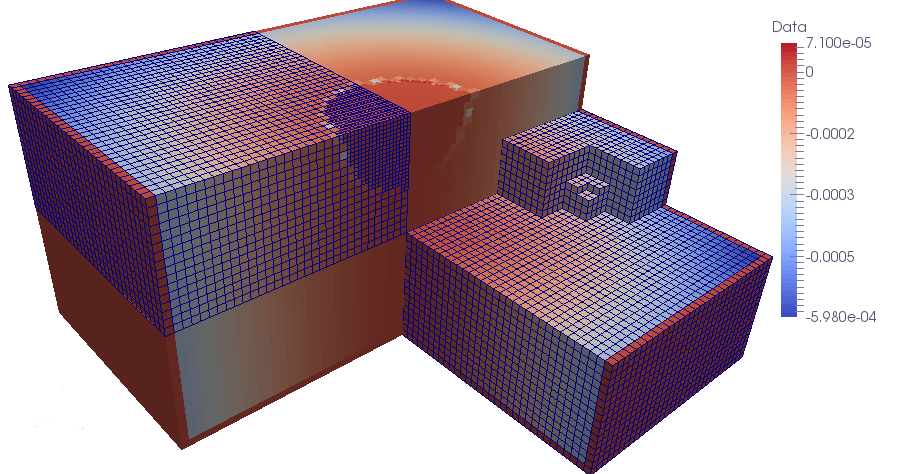
Fig 6. Penalization around a sphere of radius 0,05: section and wireframe of error distribution.
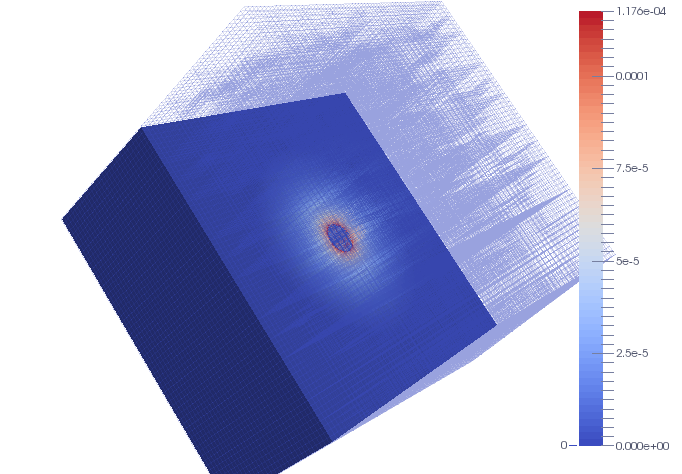
Fig 7. Three dimensional laplacian resolution, levels of jump between the subdomains equal to 3: error distribution