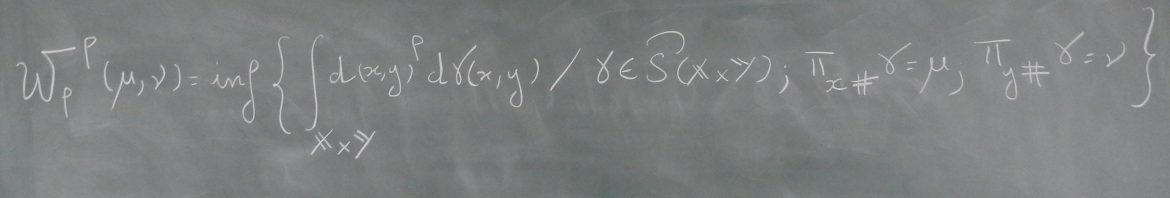Abstract: Optimal transport (OT) is a method of measuring distances between probability distributions that has found numerous applications in machine learning, computer graphics, image processing, and others. However, research has focused largely on computing transport distances quickly in great generality, and less on developing better algorithms for problems with inherent structure.
In this talk, I hope to provide perspective on how additional knowledge and constraints on the distributions or the underlying domain help in designing better algorithms. I will discuss two directions: (1) learning problems that have natural OT interpretations and lead to simple constraints and efficient algorithms, and (2) connections between the semi-discrete transport problem and classical learning problems.