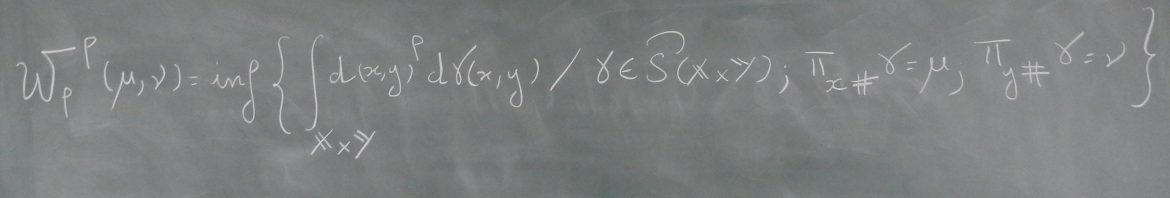Mercredi 20 mars, nous aurons le plaisir d’écouter Laurent Pfeiffer de l’INRIA Saclay ainsi qu’Anna Korba de l’ENSAE.
La séance aura lieu à 14h dans la salle Jacques-Louis Lions 2 à l’Inria Paris.
Laurent Pfeiffer (Inria Saclay)
On the Frank-Wolfe algorithm and its application to non-atomic potential games
Résumé: I will review two recent results concerning the Frank-Wolfe algorithm, an algorithm dating from the 1950 among of the very first methods for solving constrained optimization problems: following [1], I will give a dual interpretation to this method. I will give a simplified proof of convergence of the linear rate derived in [2]. In the second part of the talk, I will present two different applications of the algorithm to a class of non-atomic games (in which the impact of an isolated agent is negligible) with a variational structure, adapted from [3].
[1] F. Bach. Learning with submodular functions: a convex optimization perspective, 2013.
[2] K. Kunisch, D. Walter. On fast convergence rates for generalized conditional gradient methods with backtracking stepsize, 2022.
[3] K. Liu, Pfeiffer. Mean field optimization problems: stability results and Lagrangian discretization. Preprint, 2023.
Anna Korba (ENSAE/CREST)
Sampling through optimization of discrepancies
Résumé: Sampling from a target measure when only partial information is available (e.g. unnormalized density as in Bayesian inference, or true samples as in generative modeling ) is a fundamental problem in computational statistics and machine learning. The sampling problem can be formulated as an optimization over the space of probability distributions of a well-chosen discrepancy (e.g. a divergence or distance).
In this talk, we’ll discuss several properties of sampling algorithms for some choices of discrepancies (well-known ones, or novel proxies), both regarding their optimization and quantization aspects.