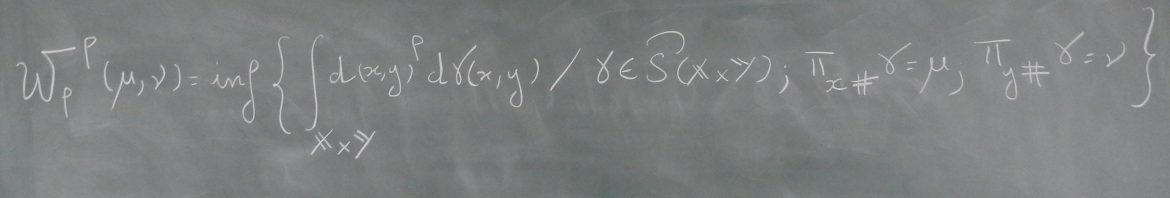Un Mokameeting aura lieu le mercredi 8 mars 2023, à 14h, dans la salle A415. Nous aurons le plaisir d’écouter Jun Kitagawa (Michigan State University).
Titre : On nontwisted optimal transport problem on nonstrictly convex boundaries
Résumé : If the cost function satisfies the so-called bi-twist condition, solutions of the optimal transport problem with absolutely continuous source measure are given by a.e. single valued maps (Monge solutions). If the cost is ambient Euclidean distance squared restricted to the boundary of a convex body, bi-twist fails. Gangbo and McCann showed if the body is uniformly convex and source and target measures are absolutely continuous with respect to surface measure, with densities bounded away from zero and infinity, there is a unique Kantorovich solution; but this may not be a Monge solution. In this talk I discuss a recent result of ours showing: when the two measures have sufficiently small optimal transport cost, the solution is given by a Monge solution, when the body is \(C^1\) and convex (but not necessarily strictly convex). This result is sharp in the sense that the claim can fail for a non-\(C^1\) domain, even if it is uniformly convex. This talk is based on joint work with Seonghyeon Jeong.