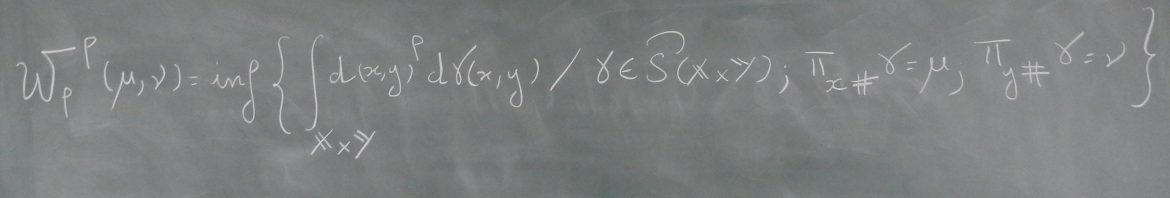Le prochain Mokameeting aura lieu le mercredi 14 avril 2021 sur Discord à 16h00.
Nous aurons le plaisir d’écouter un exposé de Stefan Steinerberger (University of Washington).
Titre : Boulangeries and the Kantorovich-Rubinstein Duality
Résumé : Suppose you want to open up 7 boulangeries so that people have to walk the least amount to get their morning coffee. That’s a classical problem in Optimal Transport, minimizing the Wasserstein distance between the sum of 7 Dirac measures and the population density. But in reality things are trickier. If the 7 boulangeries go well, you want to open an 8th and a 9th and you want to remain optimal in this respect (and the first 7 are already fixed). We find optimal rates for this problem and W_2 in all dimensions. Other W_p are more difficult and probably very interesting! All of this is also naturally related to a conjectured extension of the Kantorovich-Rubinstein duality which we discuss in detail.