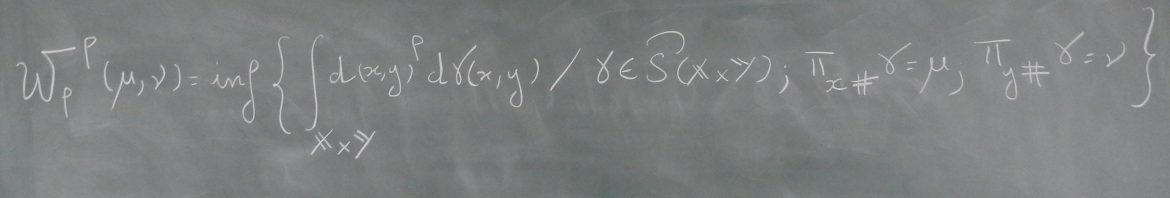Le prochain Mokameeting aura lieu le mercredi 24 mars 2021 sur Discord à 14h00.
Nous aurons le plaisir d’écouter deux exposés, l’un d’Alessandro Rudi (INRIA Paris) et l’autre d’Adrien Vacher (LIGM, U. Paris-Est Marne La Vallée)
Exposé d’Alessandro Rudi
Titre : Finding global minima via kernel approximation
Résumé : We consider the global minimization of smooth functions based solely on function evaluations. Algorithms that achieve the optimal number of function evaluations for a given precision level typically rely on explicitly constructing an approximation of the function which is then minimized with algorithms that have exponential running-time complexity. In this paper, we consider an approach that jointly models the function to approximate and finds a global minimum. This is done by using infinite sums of square smooth functions and has strong links with polynomial sum-of-squares hierarchies. Leveraging recent representation properties of reproducing kernel Hilbert spaces, the infinite-dimensional optimization problem can be solved by subsampling in time polynomial in the number of function evaluations, and with theoretical guarantees on the obtained minimum.
Given n samples, the computational cost is O(n^{3.5}) in time, O(n^2) in space, and we achieve a convergence rate to the global optimum that is O(n^{−m/d+1/2+3/d}) where m is the degree of differentiability of the function and d the number of dimensions. The rate is nearly optimal in the case of Sobolev functions and more generally makes the proposed method particularly suitable for functions that have a large number of derivatives. Indeed, when m is in the order of d, the convergence rate to the global optimum does not suffer from the curse of dimensionality, which affects only the worst-case constants.
Exposé d’Adrien Vacher
Titre : A Dimension-free Computational Upper-bound for Smooth Optimal Transport Estimation
Résumé : It is well-known that plug-in statistical estimation of optimal transport suffers from the curse of dimensionality. Despite recent efforts to improve the rate of estimation with the smoothness of the problem, the computational complexities of these recently proposed methods still degrade exponentially with the dimension. In this paper, thanks to an infinite-dimensional sum-of-squares representation, we derive a statistical estimator of smooth optimal transport which achieves a precision ε from O(ε^{−2}) independent and identically distributed samples from the distributions, for a computational cost of O(ε^{−4}) when the smoothness increases, hence yielding dimension-free statistical and computational rates, with potentially exponentially dimension-dependent constants