Numerical schemes for Low Mach flows
The numerical simulation of fluid flows at all Mach numbers is an active field of research. The occurrence of low Mach number regions in a globally compressible flow gives rise to specific numerical issues. Therefore, it is necessary to design numerical methods for compressible flows that can handle both the compressible regime (i.e. local Mach-number of order unity) and the incompressible one (i.e. very small local Mach-number).
Our goal is to solve complex flows where the Mach number has different orders of magnitude. Typical applications are atmospheric fluxes, low speed impacts and simulation of non-linear compressible elastic materials. We will study 3D phenomena involving different materials, for example viscoelastic materials, where more fast waves propagate at the same time, requiring efficient modeling and numerical simulation.
In the numerical solution of such problems, the main concern is that the schemes are usually developed for a specific regime. Our idea is to operate at the continuous level, in order to tackle the nonlinearities induced by the fast acoustic waves. In this sense we have developed two different approaches: a semi implicit one and a fully implicit one.
Fully implicit scheme
The fully implicit scheme is based on a relaxation of the non linear fluxes. The relaxation system is built in such a way that it has an entropy solution and results in a linear system of PDEs. Therefore, this method allows for an efficient and robust numerical procedure: integration schemes are simple to implement (especially since we need implicit time integration when we solve low Mach flows) and it is easier to separate fast and slow scales.
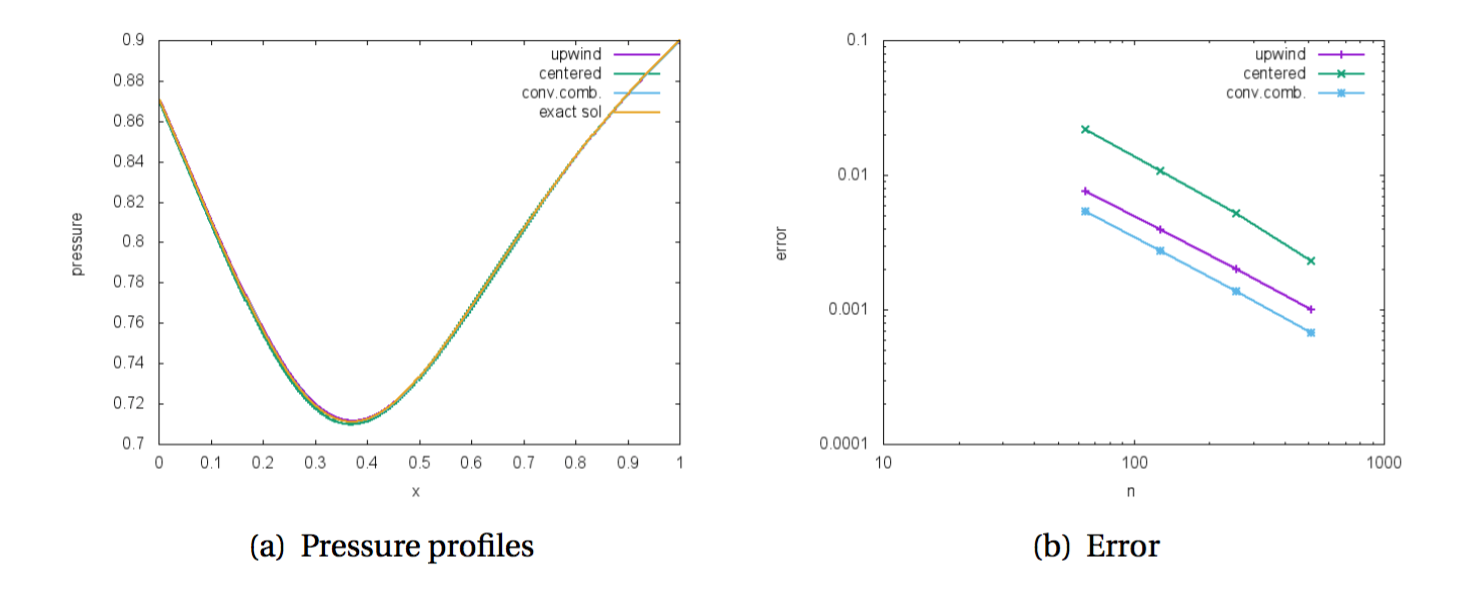
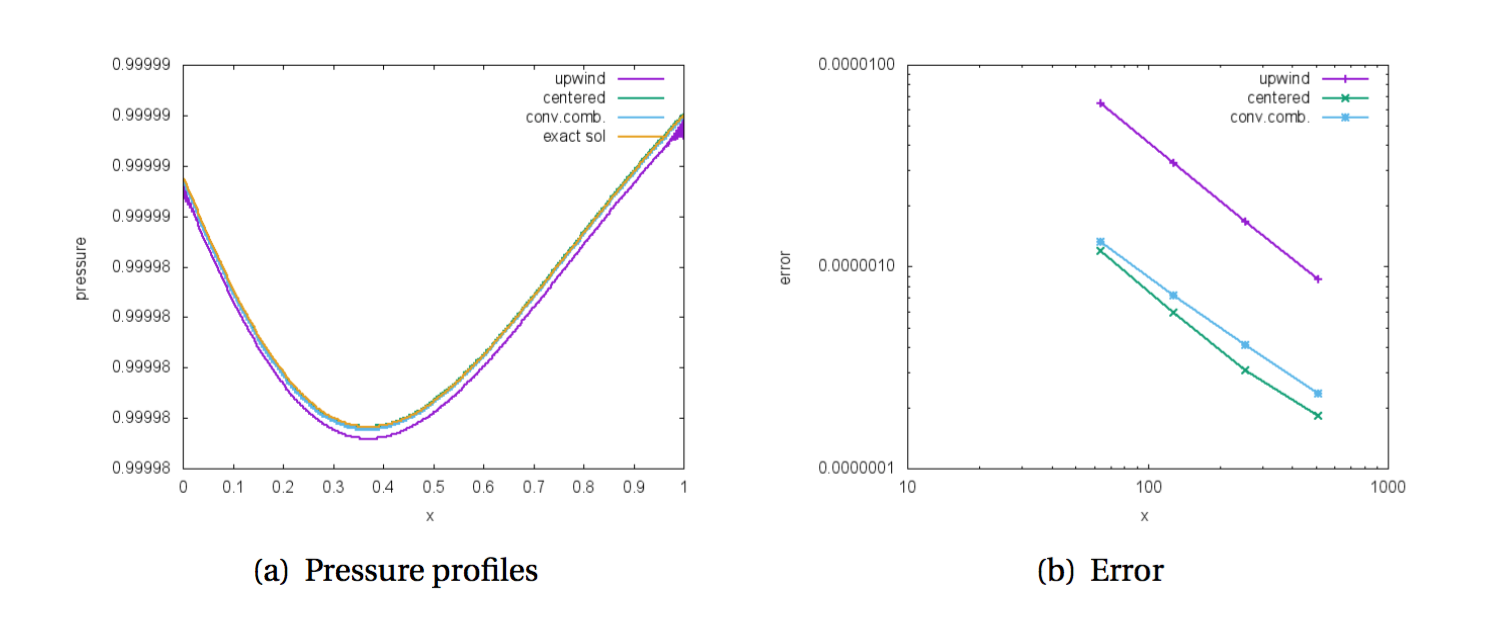
Up to now we have derived an all Mach relaxation scheme and tested it on subsonic flows inside a Laval nozzle in a quasi-1D framework. The scheme is fully implicit, therefore we do not need to deal with a very demanding CFL constraint when the acoustic waves are very fast. The spatial discretization is based on the convex combination of upwind and centered numerical fluxes. The centered part is needed to obtain the correct numerical viscosity in the case of low Mach flows. The results below show that the convex combination behaves well both for the compressible regime and and the incompressible limit (comparison of results obtained with: i)upwind fluxes, ii)centered fluxes, iii) convex combination of the two).
Semi implicit scheme
Another approach developed in collaboration with Prof. Giovanni Russo from the University of Catania filters out the acoustic waves by taking implicit the pressure terms in the Euler equations. The convective part of the equation due to the material wave is treated explicitly with an upwind scheme. This approach ends up with the resolution of a linear system on the energy.
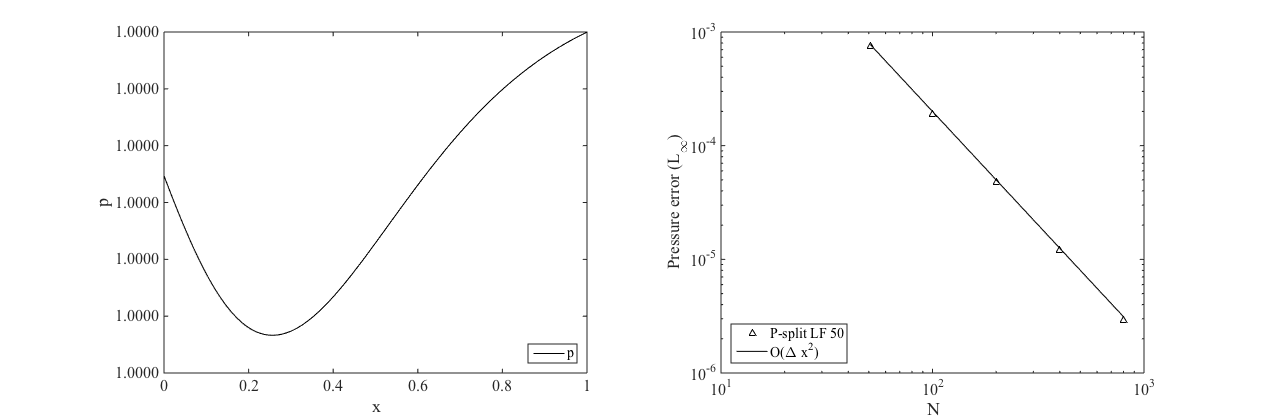
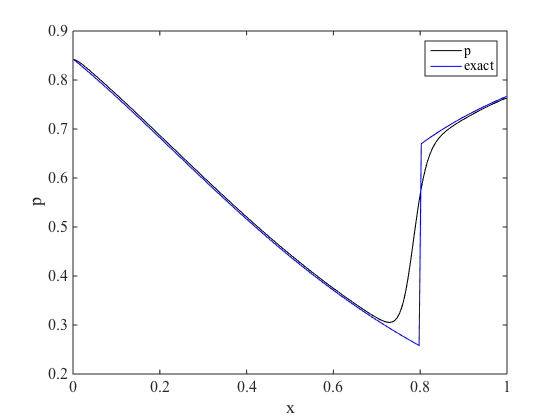
This scheme has been tested on different academic test cases such as Sod or Lax shock tube but also on more complex flows such as Laval nozzle flows in different regime from low mach to supersonic. The scheme has been proved to be accurate and stable in all regimes. Moreover, on the specific test case of the nozzle flow, a second order well-balance scheme has been developed to ensure high accuracy at steady state.