Numerical methods for hyperbolic PDEs
Hyperbolic PDEs can be used to describe fluid dynamics such as for compressible or rarefied flows. The industrial interest for such flows and the increasing computational ressources available (HPC architecture) makes the design of efficient and robust numerical schemes for hyperbolic systems an important issue.
The schemes we develop for hyperbolic systems are based on a finite volume method on Cartesian grids. The grid is fixed and immersed fronts can be considered. These fronts represent embedded solids or interfaces between different materials. With such an approach, the complexity of the work flow is transferred from grid generation (engineering work) to enforce accurately the boundary conditions (resulting in computational work). Our challenge is the design of such kind of efficient and robust schemes for hyperbolic equations suitable for HPC architectures.
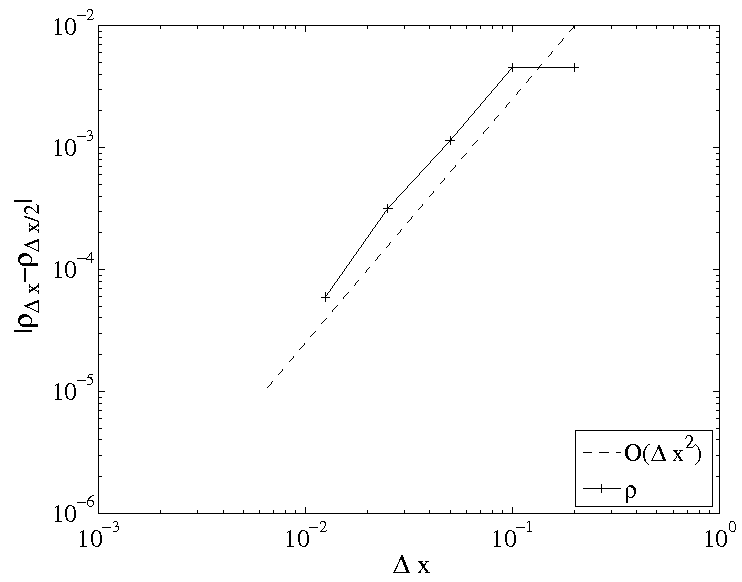
Instead of body-fitted grids, the geometry can arbitrarily cross the mesh. It is then crucial to know the position of the interface to correctly impose the boundary conditions. The tracking of the geometry position is done through a level set function (signed distance function) that can be transported in time. To compute the fluxes on a numerical interface between two grid cells of different materials, we create a ghost state such that the desired boundary condition (impermeability condition, continuity of normal velocity…) is correctly enforced. With appropriate reconstructions, second order accuracy in space can be obtained up to the immersed body. We developed this kind of schemes for compressible Euler equations or kinetic equations and we aim to extend it to octree grids and overset meshes.
-
Methods for kinetic equations
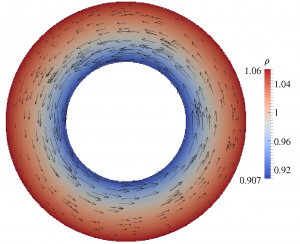
In order to deal with real applications, we develop numerical methods solving deterministic kinetic models based on the Boltzmann equation (BGK and ES-BGK models). The particularity of this equation is its high dimensionality due to the presence of a microscopic velocity space inducing a high computational cost.
Efficient and accurate schemes are developed on Cartesian grids with a particular care on the enforcement of the boundary conditions. The resulting methods are able to simulate flows in different regime (rarefied and hydrodynamic) with a second order accuracy in space.
The ongoing work concerns the extension of such methods to octree grids.
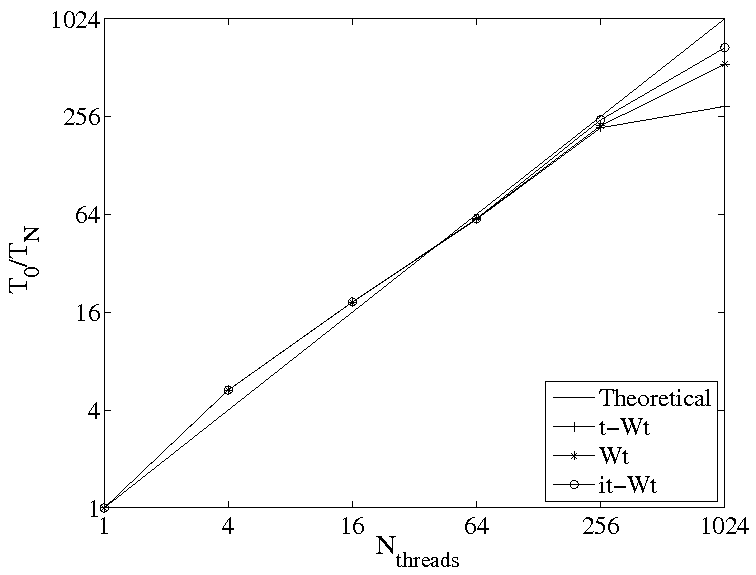
In the velocity space the Discrete Velocity Method (DVM) is used and a local grid approach is developed to improve the code efficiency with a negligeable loss of accuracy. We reached to save up to 80% of the initial computational cost with a good scalability.
- Strong scalability of the kinetic code
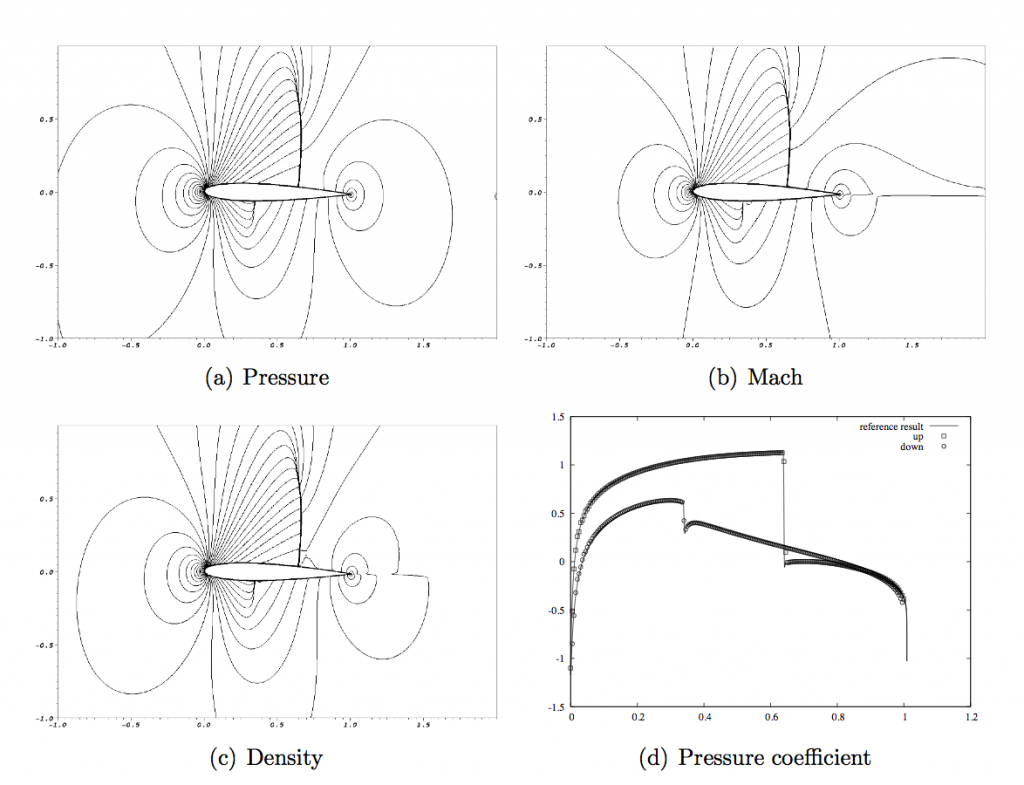
- 2. Numerical schemes for compressible flows in complex geometries
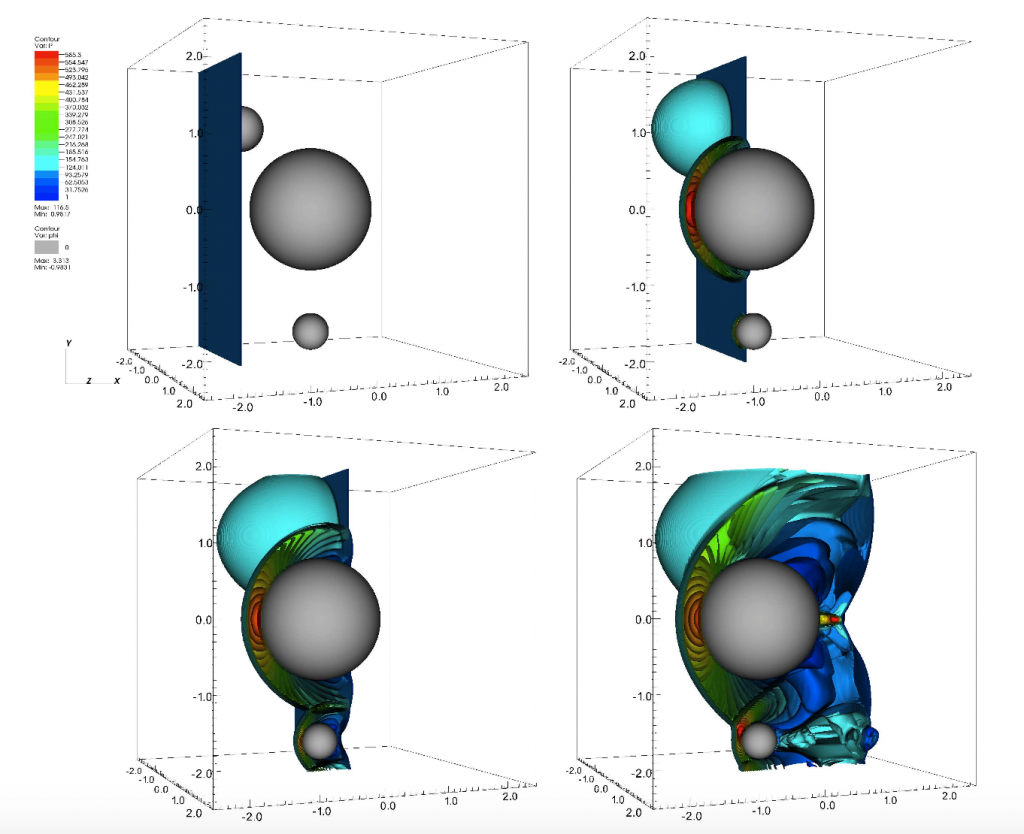
We have developed a finite-volume scheme for compressible Euler flows where the grid is cartesian and does not fit to the body. This scheme is based on the definition of an ad hoc Riemann problem at cell interfaces near solid boundaries, where the left and right states are modified in order to satisfy the boundaray conditions with second-order accuracy. It is simple to implement and does not require any special cell reconstruction at the solid wall-interface. Results show that the scheme is overall locally and globally second order accurate.