Water Networks

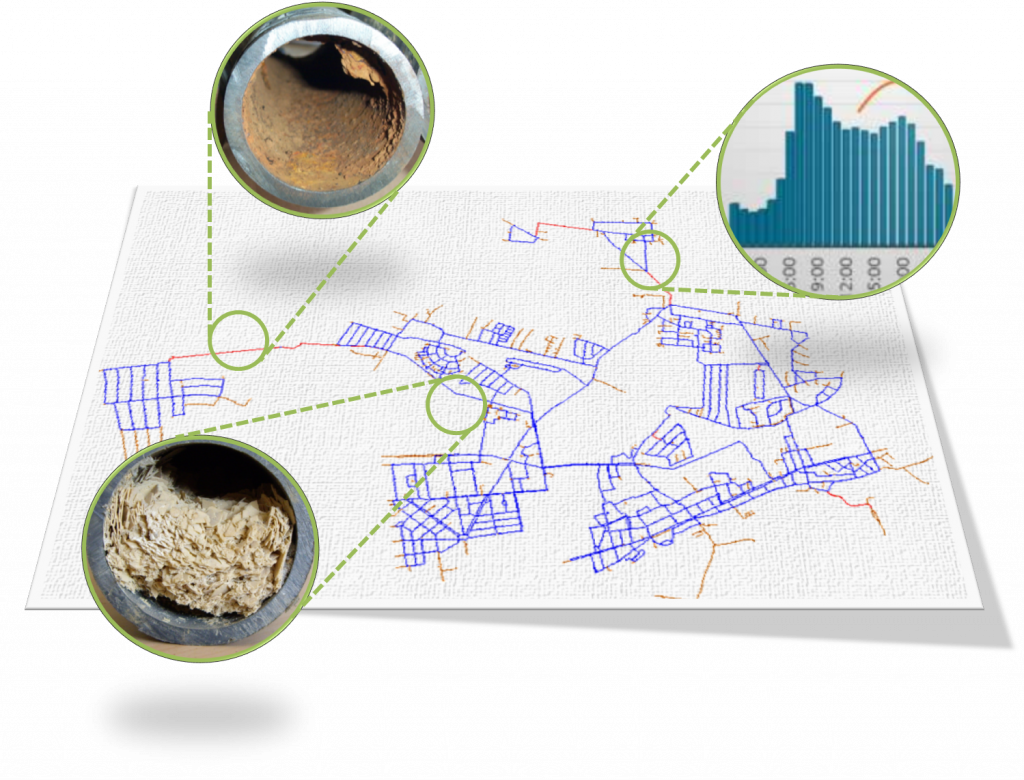
Water Networks

Reduced Order Modelling for Uncertainty Quantification

Quantifying the influence of parameter uncertainties on physical models is an important and often neglected part in the design of technical systems. Current methods for uncertainty propagation often require repeated evaluations of the deterministic system equation which may quickly become computationally too expensive. In light of this limitation we investigate a new approach in reduced order modelling to lower the computational cost of a single evaluation and investigate more efficient methods for the uncertainty propagation that reduce the overall number of required deterministic system evaluations.

Reduced Order Models

Uncertainty Quantification

The hydraulic state of a water distribution network can be calculated by a deterministic set of non-linear equations.

$$\mathbf{Aq}+\mathbf{d} = \mathbf{0} \\
\Delta \mathbf{h} (\mathbf{r},\mathbf{q}) – \mathbf{A}^{T} \mathbf{h} – \mathbf{A}^T_{f} \mathbf{h}_{f} = \mathbf{0}$$

These equations are governed by noumerous parameters like pipe-roughness and -diameter or consumer demand. In the classical deterministic models the parameters are assumed to be known exactly. The objective of Uncertainty Quantification (UQ) is to model the parameters and the quantities of interest (QoI) as random variables and evalute the effect of the uncertain parameters on the results.

Polynomial Chaos Expansion

The concept of the polynomial chaos expansion is to construct a spectral serie expansion of all random variables based on a set of orthogonal polynomials \(\Phi_k\) as a function of the basic random variable \(Z\).

$$X_P = \sum_{k=0}^{P} x_k \Phi_k(Z)$$

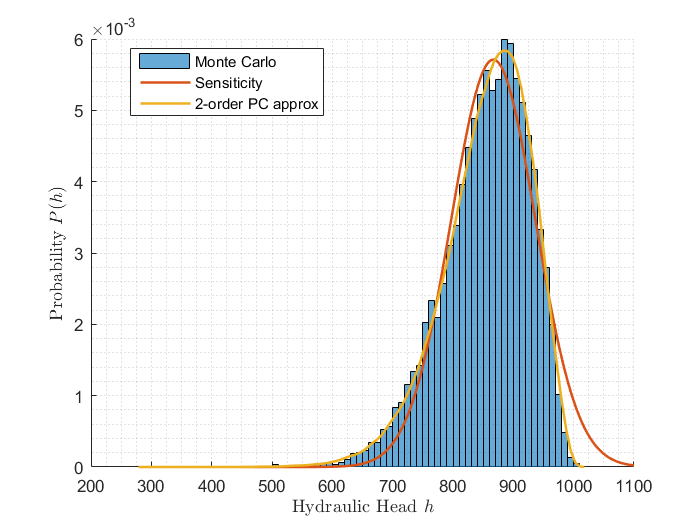
Determining the spectral coefficients of the random parameter expansion allows for the solution of the stochastic set of equations by the means of intrusive or non-intrusive spectral projection. The advantage of this approach compared to classical uncertainty propagation approaches like the perturbation method or Monte Carlo simulations lies in the combination of efficient sampling strategies and the ability to capture highly uncertain parameters with standard deviations of more than 10% in non-linear applications.

Uncertainty Analysis in Water Distribution Netorks

Using these tools we can evaluate the resulting random variables for the quantities of interest.