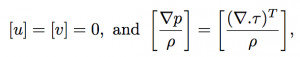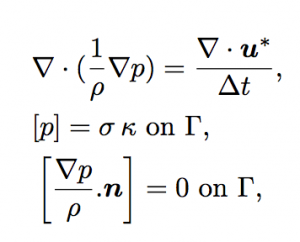Multiphase

Multiphase

For the simulation of multiphase flows with high density (and viscosity) ratios, like air-water, only few methods have been developed to our knowledge in a cartesian grid framework:
the CSF method developed by Brackbill [2], based on a regularization of the surface tension effects near the interface, and without regularization, the method of Kang et al [4],  based on the Ghost-Fluid method, the conservative cut-cell method of Raessi and Pitsch [5] and, only for fixed interfaces Zhou et al [6].

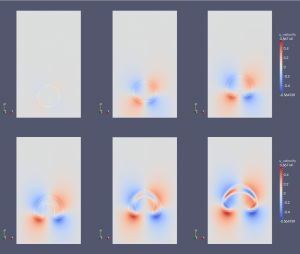
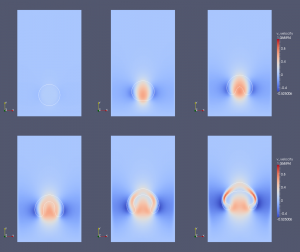
We have developed a sharp finite-differences method for the simulation of multiphase flows with high density (and viscosity) ratios [1], based on the second-order cartesian method for elliptic problems with interfaces developed in [3]. The air-water interface evolution is described by the incompressible Navier-Stokes in each subdomain (air or water):

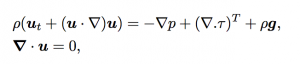with jump conditions at the interface between the two fluids, derived from:

• the velocity continuity and its material derivative :

• the balance between normal stresses and surface tension:

with the local curvature of the interface, the coefficient of the surface tension and   the viscosity.

A classical predictor-corrector algorithm is used to solve the fluid equations, in a non-incremental version, which means that the guess value for the pressure is zero discontinuous pressure values when the interface moves.
In practice, we take into account the viscous forces by following a continuous approach:  we regularize the density and viscosity values by an harmonic averaging for the computation of the viscous term in the prediction step. This approach allows for a more straightforward and robust treatment, and has been proven to provide satisfactory accuracies for high Reynolds numbers. The elliptic problem to solve in the correction step becomes therefore:

This elliptic problem is solved with the method developed in [2].

[1] M. Bergmann, F. Luddens  and L. Weynans, A sharp Cartesian method for the simulation of air-water interface, Proceedings of ICCFD8, Chengdu, China, July 14-18, 2014.

[2] J. U. Brackbill, D.B. Kothe, and C. Zemach, A Continuum Method for Modeling Surface Tension, J. Comput. Phys., 100, 335-354, 1992.

[3] M. Cisternino and L. Weynans. A parallel second order Cartesian method for elliptic interface
problems. Commun. Comput. Phys., 12(5):1562–1587, 2012.

[4] M. Kang, R. P. Fedkiw, and X.-D. Liu. A boundary condition capturing method for
multiphase incompressible flow. Journal of Scientific Computing, 15(3):323–360, 2000.

[5] M. Raessi and H. Pitsch.  Consistent mass and momentum transport for simulating incompressible interfacial flows with large density ratios using the level set method. Computers and Fluids, 63:70–81, 2012

[6]  Y. C. Zhou, J. Liu, and D. Harry. A matched interface and boundary method for solving multi-flow navier-stokes equations with applications to geodynamics. J. Comput. Phys., 231:223–242, 2012.