We have used unstructured (simplex) splines to formulate an unstructured version of isogeometric analysis. The basis functions are built from an underlying point cloud, and not on a mesh, unlike standard finite elements (FE). The basis functions are smoother than the usual FE basis, and their regularity can be adapted by aligning some points in the cloud:
Numerically, these bases retain many good properties of standard isogeometric analysis, including a better simulation timestep in time-explicit schemes, and, for the Helmholtz problem, a better precision per degree of freedom and a convergence over a larger range of frequencies.
We have used these bases to simulate the propagation of waves for geophysics, acoustic and helioseismology applications.
Multiply-connected domains
Compared to the standard, tensor-product form of isogeometric analysis, this unstructured formulation allows to model domains with holes, which is convenient for example in acoustics, such as sound propagation in a church:
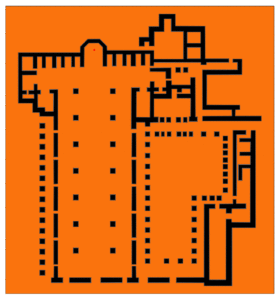Helioseismology also has to deal with complex topologies:
This kind of domains would be much more difficult to simulate using standard isogeoetric analysis, which is based on tensor-product patches with the topology of a disk
Multi-patch DG-IGA
Splines can also be defined on patches, which can be glued together using fluxes from the usual Discontinuous Galerkin methods. This way, one can include discontinuities on the simulation domain, or even coupe together (unstructured) isogeometric analysis and FE / DG schemes seamlessly in the same simulation. This is very practical for geophysics (seismic) wave propagation:
Helmholtz
Finally, using the same spline basis, one can compute Helmholtz eigenvalues for complicated shapes such as musical instruments:
or electromagnetic waveguides:
The ratio between the calculation precision and the computational cost is more favorable than standard methods, due to the smoothness and uniformity of the (spline) basis functions.
More here:
https://tel.archives-ouvertes.fr/tel-03521487
https://hal.archives-ouvertes.fr/hal-03505795/
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4057951
