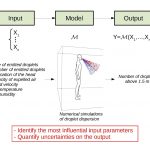
Turbulence modeling and particle dynamics are at play in numerous situations in which inertial particles are transported by turbulent flows. These particles can interact with each other, form aggregates which can fragment later on, and deposit on filters or solid walls. In turn, this deposition phenomenon includes many aspects, from the formation of monolayer deposits to heavy fouling that can clog flow passage sections. Taking into account the potentially complex morphology of these particles then requires to develop new approaches to predict the resulting statistical quantities (turbulent dispersion, formation of aggregates, nature of formed deposits, etc.).
The variety of situations (deposition, resuspension, turbulent mixing, droplet/matter agglomeration, thermal effect) involves specific models that need to be improved. Yet, one of the key difficulties lies in the fact that the relevant phenomena are highly multi-scale in space and time (from chemical reactions acting at the microscopic level to fluid motion at macroscopic scales), and that consistent and coherent models need to be developed together. This raises many challenges related both to physical sciences (i.e. fluid dynamics, chemistry or material sciences) and to numerical modeling.
Through the unique synergy between team members from various disciplines, Calisto is developing Stochastic Approaches for complex Flows and Environment to address the following challenges:
- produce original answers (methodological and numerical) for challenging environmental simulation models, with applications to renewable energy, filtration/deposition technology in industry (cooling of thermal or nuclear power plants) and filtration/deposition, dispersion of materials or active agents (such as biological organisms, micro-robots);
- design new mathematical tools to analyze the fundamental physics of turbulence;
- develop numerical methods to analyze the displacement of micro-swimmers into a range of fluids such as water, non-Newtonian bodily fluids, etc.;
- optimize and control the displacement of artificial micro-swimmers;
- develop stochastic modeling approaches and approximation methods, in the rich context of particle-particle and fluid-particle interactions in complex flows;
- contribute to the field of numerical probability, with new simulation methods for complex stochastic differential equations (SDEs) arising from multi-scale Lagrangian modeling for the dynamics of material/fluid particle dynamics with interaction.