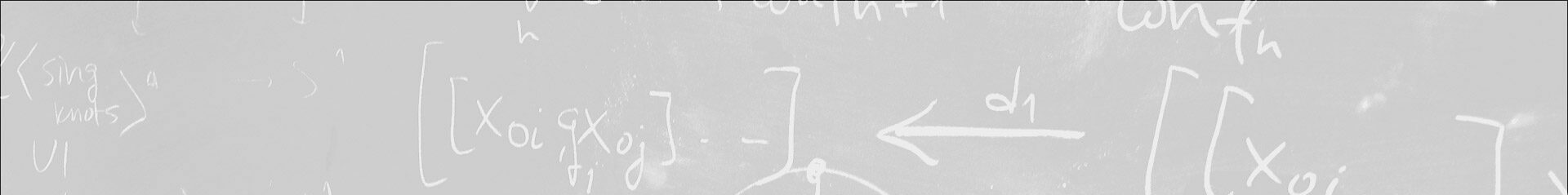Organized together with Parkas. Will exceptionally take place in salle Emmy Noether, Aile Rataud, 45 rue d’Ulm.
In Fortran/Algol tradition, a mutable variable is a variable that can be directly mutated as such by assignment, increment, etc. In contrast, ML tradition uses variables of reference types, bound to ‘boxed values’, or reference cells. These are ordinary, lambda-calculus variables that can be substituted for but not mutated. What is mutated is their value: the ‘box’. The two models seem equivalent and easily relatable. When we actually try to relate them — in the context of implicitly heterogeneous metaprogramming: writing OCaml as if it were C — we discover many subtleties, which make the problem nearly intractable. One complication is that mutable variables are not first-class, and a compositional mapping of reference-type variables to mutable variables is simply impossible.
Upon systematic investigation we discover a way to formally relate the two traditions. Practically, we can write (or generate) first-order OCaml code using reference-type variables without restrictions, and straightforwardly map it to the efficient and idiomatic C and be certain of its meaning, in C. We may hence write in (a subset of) OCaml as if it were C, using to the full extent the modules, higher-order functions and other abstraction facilities of OCaml — and obtaining all the performance of C code, benefiting from vectorization, etc. of modern C compilers.
In the Fortran/Algol tradition, the semantics of assignment such as x = x + 1 is non-compositional, and to understand it, L-values were introduced decades ago. L-values simplify assignment by taking all the complexity upon themselves. Our relation of two traditions showed L-values are not needed. What is complicated about assignment is not its semantics but an unusual syntax (sugar).