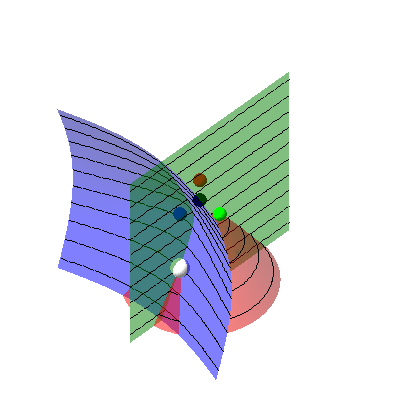
A Geometric Approach to Sound Source Localization from Time-Delay Estimates
Xavier Alameda-Pineda and Radu Horaud
IEEE/ACM Transactions on Audio, Speech and Language Processing, 22(6), pages 1082-1095, June 2014
PDF on arXiv | BibTeX | HAL | Matlab toolbox | Additional Papers | Online multimedia
Abstract: We address the problem of sound-source localization from time-delay estimates using arbitrarily-shaped non-coplanar microphone arrays. A novel geometric formulation is proposed, together with a thorough algebraic analysis and a global optimization solver. The proposed model is thoroughly described and evaluated. The geometric analysis, stemming from the direct acoustic propagation model, leads to necessary and sufficient conditions for a set of time delays to correspond to a unique position in the source space. Such sets of time delays are referred to as {\em feasible sets}. We formally prove that every feasible set corresponds to exactly one position in the source space, whose value can be recovered using a closed-form localization mapping. Therefore we seek for the optimal feasible set of time delays given, as input, the received microphone signals. This time delay estimation problem is naturally cast into a programming task, constrained by the feasibility conditions derived from the geometric analysis. A global branch-and-bound optimization technique is proposed to solve the problem at hand, hence estimating the best set of feasible time delays and, subsequently, localizing the sound source. Extensive experiments with both simulated and real data are reported; we compare our methodology to four state-of-the-art techniques. This comparison shows that the proposed method combined with the branch-and-bound algorithm outperforms existing methods. These in-depth geometric understanding, practical algorithms, and encouraging results, open several opportunities for future work.
Experimental Setup: The environment was a room of approximately 4 × 4 × 4 and we used an array of 4 microphones placed at (in meters) M1 = (2.0, 2.1, 1.83), M2 = (1.8, 2.1, 1.83) , M3 = (1.9, 2.2, 1.97) and M4 = (1.9, 2.0, 1.97). The microphones are the vertices of a tetrahedron, resulting in a non-coplanar configuration. The sound source was placed on a sphere of 1.7 m radius centred at the microphone array. More precisely, the source was placed at 21 different azimuth values, between −160◦ and 160◦ , and at 9 different elevation values between −60◦ and 60◦ , hence at 189 different directions. The speech fragments emitted by the source were randomly chosen from a publicly available data set [1].
In the case of real data the sound acquisition was performed with four Soundman OKM II Classic Solo microphones linked to a computer via a Behringer ADA8000 Ultragain Pro-8 digital external sound card. The tetrahedron-like structure was mounted onto a robotic system with two rotational degrees of freedom: a pan motion and a tilt motion. This device was specifically designed to achieve precise and reproducible movements. The emitter – a loudspeaker – was placed at approximately 1.7 meters. These recordings can be download here. In the case of simulated data, we used the timit data set and filters genrated with the ISM model of [2]. These flters can also be downloaded here.
Code: The code is pubilcly available here.
Xavier Alameda-Pineda, Radu Horaud and Bernard Mourrain: The Geometry of Sound-Source Localization using Non-Coplanar microphone Arrays, WASPAA 2013 – IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (2013) BibTex | PDF on HAL | Annex
Xavier Alameda-Pineda and Radu Horaud: Geometrically-constrained Robust Time Delay Estimation Using Non-coplanar Microphone Arrays, EUSIPCO 2012 – 20th European Signal Processing Conference (2012) 1309-1313 BibTex | PDF on HAL
References:
[1] J. S. Garofolo, L. F. Lamel, W. M. Fisher, J. G. Fiscus, D. S. Pallett, N. L. Dahlgren, and V. Zue. Timit acoustic-phonetic continuous speech corpus, 1993. Linguistic Data Consortium, Philadelphia.
[2] E. A. Lehmann. Matlab code for image-source model in room acoustics. http://www.eric-lehmann.com/ism code.html, 2012. accessed November 2011.