| About | Method | S-GCN | Download | References | Citing |
About
Processing information on 3D objects requires methods stable to rigid-body transformations, in particular rotations, of the input data. In image processing tasks, convolutional neural networks achieve this property using rotation-equivariant operations. However, contrary to images, graphs generally have irregular topology. This makes it challenging to define a rotation-equivariant convolution operation on these structures. In this work, we propose Spherical Graph Convolutional Network (S-GCN) that processes 3D models of proteins represented as molecular graphs. In a protein molecule, individual amino acids have common topological elements. This allows us to unambiguously associate each amino acid with a local coordinate system and construct rotation-equivariant spherical filters that operate on angular information between graph nodes. Within the framework of the protein model quality assessment problem, we demonstrate that the proposed spherical convolution method significantly improves the quality of model assessment compared to the standard message-passing approach. It is also comparable to state-of-the-art methods, as we demonstrate on Critical Assessment of Structure Prediction (CASP) benchmarks. The proposed technique operates only on geometric features of protein 3D models. This makes it universal and applicable to any other geometric-learning task where the graph structure allows constructing local coordinate systems.
Method
Firstly, a Voronoi tessellation of a 3D-model is computed with Voronota [1]. Then, based on the Voronoi 3D-tessellation, a graph is built. For each node of the graph, we construct a local coordinate system based on the protein backbone. Then, for each node and its coordinate system, we project all its neighbors on the unit sphere with the center in this node and compute spherical coordinates of neighbors with respect to the local coordinate system. Finally, the resulting graph is processed by Spherical Graph Convolutional Network that predicts local CAD-scores.
Spherical Graph Convolutional Network
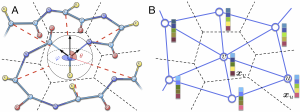
Spherical Graph Convolution Network (S-GCN) learns spherical functions (filters) that are represented as a series of spherical harmonics with trainable coefficients. For each node of a graph, filters aggregate vectors of neighboring nodes taking its local spherical coordinates as inputs. The figure A below represents some filters learned by S-GCN. The distance to the center is proportional to the absolute function value. The red color corresponds to the positive values, the blue color – to the negative ones. Histograms on the Figure B compare the ground-truth scores and the predictions of S-GCN on the CASP13 dataset
Download
The method is available in the S-GCN GitLab repository. Please follow the instructions about the installation and usage for Linux and MacOS operating systems.
References
[1] Kliment Olechnovič, and Česlovas Venclovas. “Voronota: a fast and reliable tool for computing the vertices of the Voronoi diagram of atomic balls.” Journal of computational chemistry 35.8 (2014): 672-681.