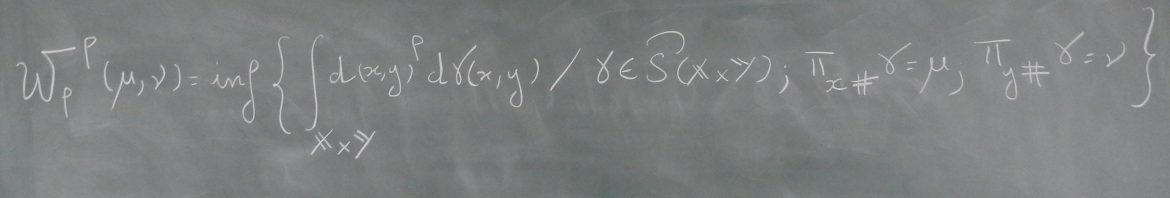Soledad Villar (New York University)
Wed. April 4th 2018, INRIA Paris, 10:00-11:00, room A215
Title: Quadratic assignment, semidefinite programming, and graph neural networks.
Abstract: Quadratic assignment is a very general problem in theoretical computer science. It includes graph matching, the traveling salesman problem, and the Gromov-Hausdorff distance between finite metric spaces as particular cases. Quadratic assignment is in general NP-hard and even hard to approximate, but in fact the problem can be tractable for a large subset of instances. In this talk we present different algorithmic approaches that lead to meaningful results for different data models. A semidefinite relaxation provides a pseudometric that can be computed in polynomial-time and has similar topological properties to the GH distance. A projected power iteration algorithm succeeds at aligning noisy networks. And a graph neural network can actually learn an algorithm to solve network alignment and the traveling salesman problem from solved problem instances.
Bibliography: A note on learning algorithms for quadratic assignment with graph neural networks. Soledad Villar, A. Nowak, A. S. Bandeira and J. Bruna (ICML 2017).