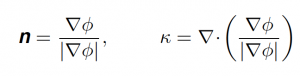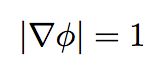Level Set
In multiphysics flows (multiphase flows, fluid-solid interactions), it is essential to accurately track and represent the evolution of interfaces. Moreover, the accurate computation of geometric properties of the interface is often required: for example, the computation of the normal to the interface for methods with second-order penalty terms in fluid-solid interactions [1] or for computations on numerical domains that do not fit the physical domain [4] For the cases of multiphysics flows where the surface tension plays an important role, accurate computation of the curvature is a key stone.
In an Eulerian framework, an efficient way of capturing interfaces is the level set method, introduced by Osher and Sethian. It consists of the implicit capture of an interface through the zero-isocontour of a higher dimensional function. This eases the treatment of topological changes and can easily be carried on in parallel codes, using domain decomposition for example.
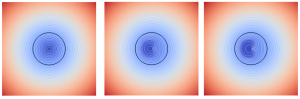
 Example of a level-set function and the interface associated
Example of a level-set function and the interface associated
Moreover, geometric properties as the normal to the interface and the curvature can be expressed with first or second-order derivatives of this level-set function:
Distortions of the level set function might lead to significant errors in computing the geometric properties, and one possible way to avoid these errors is to use the distance function as a level set function. However, even with a distance function as an initial state, the level-set can derive far from the distance function. To circumvent the problem, Sussman et al. introduced a reinitialization algorithm, i.e. an algorithm capable of recomputing the distance function. Several methods have been developed over the years to perform the reinitialization step. They are based on the resolution of the eikonal equation:
either by a relaxation method or using a Gauss-Seidel based method as in fast marching methods or fast sweeping methods. The relaxation methods can provide high order accuracy on the level-set function but are CPU consuming. The fast marching or fast sweeping methods are on the contrary much quicker, but might suffer from a lack of accuracy.
We have investigated in [2] a level set technique that ensures a good representation of the interface, as well as its geometrical properties, even for long times. The method is developed in a finite differences framework on cartesian grids, in such a way that parallelization should be easily and efficiently available. It is based on a coupling between an upwind iterative algorithm near the interface [3] , and a second-order fast-sweeping algorithm elsewhere. The strategy is based on a limited number of reinitialization steps:
- The cost of one reinitialization step is quite low, but with a good accuracy for the computation of geometric properties. For example, we have shown examples where the total number of iterations during the reinitialization procedure does not exceed 40, even on a 1280 1280 mesh, while the relaxation method alone would have required nearly 2000 iterations.
- The number of reinitialization steps is controlled by the distortion of the level set itself, so that reinitialization only occur when flat or steep gradients are created.
Numerical results compare well with usual level set strategies and confirm the necessity of the reinitialization procedure, to prevent the creation of small and/or large gradients near the interface. Moreover, compared to usual level strategies that involves either an incomplete reinitialization and/or a number of reinitialization steps that depends on the mesh size or the time step, this method exhibits a third order accuracy on the level-set function itself, and then a first order accuracy on the curvature.


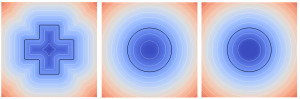 Evolution of the interface under mean curvature flow: without redistanciantion (top) and with new redistanciation (bottom)
Evolution of the interface under mean curvature flow: without redistanciantion (top) and with new redistanciation (bottom)
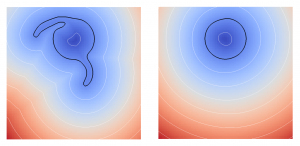
Vortex test case at final time with small time steps: with classical redistanciation (left) and with new redistanciation (right). The circular shape is more preserved with the new redistanciation
[1] M. Bergmann, J. Hovnanian, and A. Iollo. An accurate cartesian method for incompressible flows with moving boundaries. Commun. Comput. Phys., 15(5):1266–1290, 2014
[2] M. Bergmann, F. Luddens, L. Weynans, Enablers for high order level set methods in fluid mechanics, submitted, INRIA Research Report RR-8656
[3] A. du Chéné, C. Min, and F. Gibou, Second-order accurate computation of curvatures in a level set framework using novel high-order reinitialization schemes. J. Sci. Comput., 35(2-3):114–131, 2008.
[4] Y. Gorsse, A. Iollo, H. Telib, and L. Weynans, A simple second order cartesian scheme for compressible Euler flows. J. Comput. Phys., 231(23):7780–7794, 2012
[5] M. Sussman, P. Smereka, and S. Osher. A level-set approach for computing solutions to incompressible two-phase flows. J. Comput. Phys., 114:146–159, 1994